اجابات الفصل األول الفرع العلم والصناع 1
|
|
|
- جدير المؤقت
- منذ 6 سنوات سابقة
- المشاهدات:
النسخ
1 اجابات الفصل األول الفرع العلم والصناع
2 حلول الوحدة االولى / حساب التفاضل تمار ن )-( صفحة السؤال األول: أ( ممدار التغ ر ف ق)س( = ق) 5 ( ق) ) = 7 ب ) متوسط التغ ر لاللتران ق)س( السؤال الثان : متوسط التغ ر لاللتران ق)س( ف الفترة 5 ()r ()r عندما تتغ ر س من الى ساوي = ( )r ( )r 9 5 h ( 6) h h ()r (h)r h h h ( h)( h) h9 h h السؤال الثالث :متوسط التغ ر وبالتال ومنها h 9h9 5 ومنها h )مرفوض ألن أ ( h = ف الفترة السؤال الرابع : متوسط التغ ر لاللتران ن )س( ()r ()r (()r ()r)8 (()r ) ()r9 (); (); 6 ()r ()r السؤال الخامس: م ل المستم م ل = () () متوسط التغ ر ف االلتران () ()r ()r 8 ( ()r) 9 ()r السؤال السادس: السرعة المتوسطة ف الفتر ة (f ) f 9 ()t ()t 6 ومنها ب + 8= وبالتال ب=
3 (f ( k)h) السؤال السابع: متوسط التغ ر لاللتران ق )س( ([ f h) [ kf k h ()r (k)r k k ( k)f ( k)h (f ( k) h) k k k = السؤال الثامن :أ( متوسط التغ ر ف االلتران ق)س( عندما تتغ ر س من إلى ()R ()R ()r ()R = ( ) ب( متوسط التغ ر لاللتران ق)س( عندما تتغ ر س من k ( k ) إلى k = ()r ()r ن =- ومنها ن - = - وبالتال تمار ن )-( صفحة 6 ( )r ( )r = ( ) r السؤال األول: ( ) ( ) ()r ( )r السؤال الثان :أ( () r
4 9 w w] ] ب( () r ج( عندما س= نالحظ أن: ق)س( غ ر من لاعدته ومنها ()R ()R () r ( ) r ( ) r = ( ) r فإن u ()r (u)r u u عندما س = أي ان ( ) r السؤال الثالث : ف الفترة u u () r u u u u u ( u) ( )( u) u u (u ) u u ()r (u)r u () r u u u u u : ف الفترة السذتقة غيخ مؾجؾدة ( أط اخؼ فتخة ) عشجما س= -
5 عشجما س = السذتقة غيخ مؾجؾدة ألف () r () r السذتقة فتكؾف بإيجادىسا كذلػ باستخجا تعخيف () r الدؤاؿ ال اخبع : أفخض العخض س فيكؾف الظؾؿ س كمشيا السداحة l / س معجؿ التغيخ في مداحة الرفيحة )عشجما س = 6 ) سؼ 8 (6)l ()l 6 6 () l 6 6 6l = ) )بفرض و= 5 5 ()r (5 )r () r السؤال الخامس :أ( ()r ()r ()r ()r () r ()r ()r ب( بمسمة البسط والممام على )س- ( ()r (9 )r () r9 = ()r (9 )r ج( 6 9 )بالضرب بالمرافك والتبس ط ) 5
6 ()r ( )r ()r ( )r (()r ( )r) ()r ( )r ( )r ( )r = ()r ( )r ()r ( )r 6 () r () r 5 د( بالفرض لكل حالة ()r ()r ()r ()r ()r ()r ه( () r ()r تساريؽ )-( صفحة 55 (()r ()r) ( )()r = 7 5 ( ) r 5 السؤال األول : أ( () r ومنها ( ) ( ) ب r) () ومنهاr ( )7 6 () ومنها ( ) r ( 5) ( 5) () r ج ) () () () () () r () ( r) السؤال الثان : أ( () () () r= () () () r 9 = 6
7 () () () () r () r = () () ()r ب( ق) (= () 9 () r () r () = ج( () r () ()() r () r () نجد () r مؽ اشتقاؽ ()r ح ث () r ميل السساس = عل ال ادكية التي يرشعيا السساس مع االتجاه السؾجب لسحؾر الديشات () 5 = () () r كمشيا بالتعؾيض يشتج أف: w ( ) w ( ) ( ) السؤال الرابع: أ ) ( ) ( ) ( ) الطرف األ من = = الطرف األ سر h5 w 5 5 h w 5 ب ) 6 6 ( 5 h) 6 h h w w 5 ( 5 h) w ومنها () r ومنها ( ) ()r 6 () r ومنها () r السؤال السادس : أوال: ()r () r أ( السؤال الخامس :بعد التبس ط 7
8 ب( () غ ر موجودة ألن ه)س( غ ر متصل عندها () ج( r الحظ ان االلتران الجد د متصل عندما س = () ( r) د( الحظ أنه ال مكن تحد د وجود باستخدام مشتمة حاصل الضرب ومنها r) () ( () ( r) ثانيا : ندتشتج أنو ال يسكؽ الحكؼ عمى كجؾد أك عج كجؾد السذتقة باستخجا قؾاعج االشتقاؽ لحلػ نعؾد إلى إيجاد قاعجة االقت اخف األصمي ثؼ نحجد كىحا ال يتشاقض مع القاعجة السحكؾرة. h () r k ( k)k () r () h6 () r h ()r الدؤاؿ الدابع : h6 () r () 5h ومنها 8 h6 () r () r k ()r k k السؤال الثامن : k ومنها k k h ( k)( k)k () r h لكن h ( k)( k)k ومنها u نفرض س = ع ومنها u السؤال التاسع : عندما س ف نإ () r (u) r 5 () r u u = () r (u) r u u النها ة = 8
9 )- صفحة 9 تمار ن ( أ( السؤال األول : w] ] ( )( )-( -)( ) w] ( ) ( ) ] w] ( ) ] ( ) w] ] w] ] ب( ج( د( السؤال الثان : ) تم التعامل مع مشتمة على أنها حاصل ضرب( ( w )w ( ) = w ] ] w] : ] w ] ] w w] w ] ] اآلن الطرف األ من= ] السؤال الثالث = )مع التبس ط واالختصار ) () r السؤال الرابع : r () ومنها = (w) ( w) = ( ) ( ) w w = (w السؤال الخامس : = 9
10 تمار ن )5-( صفحة 6 وناتج التعو ض = السؤال األول : ا( ناتج التعو ض = ب( ناتج التعو ض = وبالتال ل مة النها ة = وبالتال ل مة النها ة= ج( ناتج التعو ض = نطبك لاعدة لوب تال لوب تال مرة أخرى فتصبح وبالتال ل مة النها ة = مرة اخرى فتصبح وناتج التعو ض تطبك لاعدة 6 6 السؤال الثان : ] w] أ( w] ] ب( w ومنها 5 w] ] 5 5 w ج ) ومنها ( )( ) w د( ] ومنها h ()r ()r h ومنها w] ( )( ) ( )( ) ] h w] السؤال الثالث : متوسط تغ ر االلتران ص w w السؤال الرابع : ومنها كبحل السعادلة يشتج أف: س =
11 k k k k السؤال الخامس :بما أن ناتج التعو ص نستخدم لاعدة لوب تال lk h k h k k h l l l l l l h l h h h الحظ أن ناتج التعو ض () r ()r r ()r ل مة النها ة = السؤال السادس : )6- صفحة تمار ن ( م ل المماس = السؤال األول: م ل المستم م = م ل المنحنى = م ل المماس ومنها نمطة التماس = ألنه عمودي عل ه. () r السؤال الثان : ) w ( ) r ميل السساس= ومنها نمطة التماس ومنها ( )r ( ) معادلة المماس w ()r م ل المماس= r () w () r ( ) w السؤال الثالث : معادلة السساس ىي السساس يقظع محؾر الديشات في الشقظة ب كمشيا كالرادات في الشقظة جػ ) مداحة السثمث fl ج كحجة مداحة
12 k 8 h 6 () r ( ) k السؤال الرابع : م ل المماس 6 6 () r ( ) 6 س =8 أك س= - h م ل المماس = كبحل السعادلة يشتج أف: عشجما س= 8 ص = كعشجما س=- ص =5 الدؤاؿ الخامذ : أقرى ارتفاع عشجما الدخعة = صفخ أي أف: كمشيا (k)t 8 l8 ()t السدافة الكمية السقظؾعة أي يكؾف الجدؼ عمى ارتفاع 66 كىؾ نازؿ / ث تيسل k كمشيا k 6 (k)t 6 k5 k سخعة الجدؼ في المحغة السظمؾبة = 6 l k5 k (k)t k السؤال السادس : أ( أقرى ارتفاع عشجما الدخعة = صفخ ومنها ث l5 k (k)u ()t أقرى ارتفاع = ب( عشجما يكؾف الجدؼ عمى مدتؾى سظح العسارة تكؾف ال ازحة =l كمشيا ث ن= تهمل k = k5 k الدخعة في تمػ المحغة)ف= ( / ث أ( السؤال األول : تمار ن ) 7- (صفحة 8 ( ) ( ) ] ( ) () w] : 9 ] w] ومنها w ] w] : ] w] عندما س= ب( عندما س=
13 w] u u] 7 u5 w u] ] u ( ) u u] w] w] ( ) ( ) ] u] ] 5 w] : ] w] ] ج( عندما س= w] ] : د( عندما س= w] ه( ( ) ] w] ] عندما س= : () l ()l ()l () r السؤال الثان : () l ()l ()l () r ( ) () r 6 ع () السؤال الثالث : أ( ب( ( )l ( ) l () r السؤال الرابع : ( ) l ( ) l 6 ( ) l ( ) l () r () r
14 ( ) r () r() r ] w] السؤال الخامس : w] ] : عندما س= ( ) r 8 w ) () r السؤال السادس : ومنها نمطة التماس معادلة العمودي ه 5k w] k] ( ) r م ل العمودي السؤال السابع: 7 5 w] k] k] ] عندما ن= : أ ضا 7 k] w] w] ] k] ] عندما ن= : f h w السؤال الثامن : f h w f f h h w ( f f h h ) w f h f h w f h ( f h w w w w () () r () (()) r () ( r) ( ) r () ( r) ( ) () ( r) السؤال التاسع:
15 السؤال العاشر : نفرض م = س ف كون (l) ( l) () ( ) l (l ) (r r) rl rl r rl ] نتج أن: r r r r l l r wl rl w r. r w l ومنها r w l l l l l l w] السؤال الحادي عشر : بالضرب والمسمة على تمار ن )8-( صفحة 5 w w w أ( السؤال األول : ومنها ww w w ( ) ( )) 5 5 w] 5 5 ] ب( 5 w ج( ( w )(w ) w بالتبديط يشتج أف: (w ) w (w ) w w w ومنها w 6w ومنها 5 w 5 : نجج نقط التقاطع w د( الدؤاؿ الثاني عندما ص= -6 ال وجد س عندما ص= 5 فان س= ( ) 5 w م ل المماس عندما س= ساوي w] ] م ل العمودي أي ومنها معادلة العمودي ه 6 w 5
16 () 5w م ل المماس عند ما س= ساوي م ل العمودي ومنها معادلة العمودي ه 5 w الدؤاؿ الثالث : باالشتقاؽ الزسشي يشتج أف: kh kh t] t k] (k)u kh h ومنها ومنها (l k) h u h kh t] k] h ()u t السؤال الرابع : t (l k) h t (l k) h j الدؤاؿ الخامذ : نفخض نقظة التساس )س ص( الحظ اف الشقظة السعظاة خارجة عؽ مشحشى العالقة ومنها w 8 w w ww 8 8 w w نمط التماس ه ) ( ) ( w w w w w w ) ومنها السؤال السادس: عند النمطة بالتبس ط نتج أن : كون w w السؤال السابع : باالشتماق نتج أن: w w ومنها w w 6
17 د ب صفحة 5 ب ج ا السؤال األول : تمار ن عامة ( الوحدة االولى( 9 8 د د د أ ب أ ج د ج ()r ()r ()r ( )r األسئلة الممال ة: السؤال الثان : متوسط التغ ر لاللتران ص = ( ) r( ) ( ) r( ) السؤال الثالث : () r مكن الحل باستخدام الفرض والمسمة. السؤال الرابع: أ ) بالتعو ض داخل النها ة كون الجواب وبالتال : ب( بالتعو ض داخل النها ة كون الجواب وبالتال : بالتعو ض المباشر كون الجواب وبالتال : ج ) 7
18 بالتعو ض المباشر كون الجواب وبالتال : د ) وبالتعو ض المباشر نتج أ ضا ونكمل تطب ك لوب تال ( ) ( ) ( ) ( ) السؤال الخامس : أ( () r باالضافة والطرح مكن استخدام لوب تال ف ا جاد النها ة ()r () r w بفرض ب( () r () r متوسط التغ ر ف االلتران () 6 9 ()r ()r 9 () () 5 ()r ()r ()r () r : السؤال السادس: السؤال السابع ق)س( متصال عند س = ألن ()r () r ()r ()r 9 ()r () r k الدؤاؿ الثامؽ : نفخض أف زمؽ كصؾؿ كخة ن ادر ك زمؽ كصؾؿ كخة أحسج ف+ k5 k5 ( كمشيا k)5 (k) t ( k) t 8
19 5 5 () t زمؽ كصؾؿ كخة ن ادر k سخعة ارتظا كخة ن ادر م/ ث () ( ) السؤال التاسع r: h () ( ) (( ) ( ) r (( )r) ( ) (r ) h h h ومنها ( h ) ( h ) ومنها ومنها ( h ) س= 5 السؤال العاشر : الحظ أف: ؽ)س( مشفرل عجما س= عند غ ر موجودة. () r ( ) k k ( ) t السؤال الحادي عشر : k k t ( ) j k k ( ) u () r 9 السؤال الثان عشر : 6 6 () r 6 6 () r 6 6 ( ) r ( ) ( )8 ( ) ( ) () r السؤال الثالث عشر : أ ) (( ) ( )8) ( ) ( ) () r تهمل (7 ) ( ) ( ) () r ( ) () r ب( كبحل السعادلة يشتج أف القيسة السظمؾبة ىي
20 6 6 6 ( 6 ) w] ] ( ) w] (k k )h (k) t السؤال الرابع عشر : ب( أ( ] السؤال الخامس عشر : (k k ) h (k) t u (k k ) h (k) t j (k k )h (k) t j م/ ث 5 () r. ( ) ( ) السؤال السادس عشر : النماط ه حلول الوحدة الثان ة/ تطب مات التفاضل ) صفحة 65 تساريؽ )-5 الدؤاؿ األكؿ : أ( ()r عمى الفتخة نبحث في شخكط نغخية ركؿ عمى ؽ)س( في ؽ)س( مترل عمى () r ؽ قابل لالشتقاؽ في () r ؽ) 6 (= صفخ ؽ) ( = صفخ ؽ) 6 ( = ؽ) (
21 [ r [ ([) r [ تحققت شخكط نغخية ركؿ كمشيا يؾجج [ [ [ [ ب( عمى ()r الفتخة الحل: ()r ؽ)س( مترل عمى ؽ)- ( = ؽ) ( =صفخ كقابل لالشتقاؽ عمى إذف تحققت شخكط نغخية ركؿ عمى ؽ)س( في ألنو كثيخ حجكد كمشيا يؾجج () r [ [ ()r ج( الحل: نبحث في شخكط نغخية ركؿ عمى االقت اخف ؽ)س( في الفتخة ؽ)س( مترل في النو اقت اخف لؾغخيتسي كالفتخة ضسؽ مجالو () r ؽ)س( قابل لالشتقاؽ في الفتخة 5 ( )r 5 ()r ()r ( إذف r( تحققت شخكط نغخية ركؿ عمى االقت اخف ؽ)س( في الفتخة ([) r [ إذف
22 = صفخ كمشيا جػ= [ [ [ [ [ [ كعشجما إذف [ [ ) - الحظ اف جػ = )تيسل د( ()r الحل: نبحث في شخكط نغخية ركؿ عمى ؽ)س( في ؽ)س( قابل لالشتقاؽ عمى الفتخة بحيث ؽ)س( مترل عمى () r ( )r ؽ) 6 ( 5=( )r ؽ) 6 ( = صفخ إذف لؼ تتحقق شخكط نغخية ركؿ قج يؾجج ج [ [ صفخ = [ r [ [ [ [ [ [ [ [ )تيسل ) [ [ [ اك الدؤاؿ الثاني: ()r أ( ()r مترل عمى كثيخ حجكد قابل لالشتقاؽ عمى الفتخة ()r () r إذف تحققت شخكط نغخية القيسة الستؾسظة عمى ؽ)س( في الفتخة r r ([) r [
23 ( تيسل ) 5 6 [ [ [ [ ()r ب( نبحث في شخكط نغخية القيسة الستؾسظة عمى ؽ)س( في [ ؽ)س( مترل عمى () r ؽ قابل لالشتقاؽ في إذف تحققت شخكط نغخية القيسة الستؾسظة بحيث [ [ كمشيا ]= - تخفض كمشيا قيسة ج السظمؾبة ىي الرفخ 9 r r ([) r [ [ ]=صفخ أك [ 9 ج( ()r الحل : نبحث في شخكط نغخية القيسة الستؾسظة عمى ؽ)س( في 9 ؽ)س( مترل في 9 كقابل لالشتقاؽ في 9حيث () r إذف تحققت شخكط نغخية القيسة الستؾسظة عمى ؽ)س( في r 9 r ([) r 9 [ 9 5 [ 5 [ 5 [ 9 5 [ 5 [
24 الدؤاؿ الثالث: يحقق شخكط نغخية القيسة الستؾسظة h F = ()r إذف ؽ)س( مترل عمى ؽ مترل عمى كقابل لالشتقاؽ عمى r r 6f h f 8 h f h h () r f f h ( ) r ( ) r )5( ) ك كبحل السعادلتيؽ ) f h f h 8 f h ػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػػ 6 r r 7 ([) r f 8 f h h ليجاد قيسة جػ : [ [ 7 5 [ 5 تخفض عشجما [ [ [ 7 6 [ [ عشجما ال اخبع: الدؤاؿ fh [ باستخجا نغخية القيؼ الستؾسظة اف أثبت fh f h ()r البخىاف : نبحث في شخكط نغخية القيسة الستؾسظة عمى ؽ)س( في
25 (h)r (f)r ([) r h f س fhألف f h [ f h r ؽ)س( مترل ألف قابل لالشتقاؽ عمى () r إذف تحققت شخكط نغخية القيسة الستؾسظة كمشيا بحيث f h h f h ffh [ h f [ fh [ fh كىؾ السظمؾب [ 8 () r الدؤاؿ الخامذ : البخىاف : نبحث في شخكط نغخية ركؿ عمى ؽ)س( في ؽ)س( مترل عمى كقابل لالشتقاؽ عمى بحيث [ r r r بحيث [ = صفخ r ؽ) 6 ( = صفخ إذف تحققت شخكط نغخية ركؿ ؽ)س( مساسا أفقيا كاحجا عمى االقل في عشج س= جػ ليجاد نقط التساس: صفخ كىحا يعشي اف لالقت اخف fh [ [ 8 ([) r [ [ [ اك [ ألف القيؼ األخخى جػ= 6 جػ= تخفض إذف نقط التساس ىي الدؤاؿ الدادس: مترميؽ عمى الفتخة كقابميؽ لالشتقاؽ عمى h f [ r fu hu f h [ fh r f h r u الفتخة fh h f f h أثبت أنو البخىاف: نبحث في شخكط نغخية القيسة الستؾسظة عمى ؽ)س( في 5
26 س- fh ؽ)س( مترل عمى fh كقابل لالشتقاؽ عمى تحققت شخكط نغخية القيسة الستؾسظة مؽ السعظيات hr fr [ r f h [ h f fr hr [ لكؽ f h h f إذف r h f fu hu [ r h f fu hu h f [ r كىؾ السظمؾب الدؤاؿ الدابع: البخىاف ()r: )r )مترل عمى كقابل لالشتقاؽ عمى ( )r ()r ( ؽ) 6 ( =صفخ r( [ r إذف تحققت شخكط نغخية ركؿ كمشيا [ [ [ [ r ]ا r كمشو r كبالتالي [ [ القيسة التي تعيشيا الشغخية ىي عشجما تمار ن )-( صفحة 7 السؤال االول: س -[ ] 5 أ( ق)س(= س () r الحل : ق)س( متصل على ]- ] 5 6 () r صفر= س )- س( اشارة - 5 6
27 س= صفر أو س = من اشارة () r فإن ق)س( متنالص ف -[ ] [ ] 5 ومتزا د ف [ ] ب( () r () r الحل: ()r متصل ف اشارة () r من اشارة ( )فإن r متزا د ف ()r () r ج( ()r p الحل: ()r ()r متصل على ح () r ()r من اشارة () r فإن متنالص ف ومتزا د ف د( () r 9 الحل: () r 9 متنالص ف ومتزا د ف ()r السؤال الثان : اشارة اشارة () r () r ح () r الحل: () r ومنها وبالتال متزا د على اشارة ومنها ق متزا د على الفترة 7
28 السؤال الثالث: ()r الحظ ان ق غ ر متصل عند س= الن ()r ()r النها ة غ ر موجودة اشارة () r موجبة دائما وبالتال () r غ ر موجودة () r () r لجم ع ل م س ف المجال () r و متزا د ف متزا د ف ()r السؤال الرابع : () () r (); ()r () () () r () r () ; اشارة () () () r()r () ; الحل : ()r () () ()r (); () ; ;( )متزا د ف السؤال الخامس : متنالص ف ( ) ( ) ن متصل على ح النه كث ر حدود اشارة ( ) ( ) ( ) الن () r كون ق متزا د ( ) ( ) متزا د ;( )متنالص عندما (); 8
29 السؤال السادس : متصل ن ف كث را حدود ف ولابل ن لالشتماق ف () ()r الحل : () r متنالص ف مجاله اذن ()r ()r مع منحنى ()r ف الربع الرابع اذن () متزا د ف مجاله اذن () () مع منحنى () لكن ف الربع االول اذن () () r () ()r () ()r سالب موجب + موجب سالب = سالب () ()r اشارة اذن () ()r متنالص ف () r () r السؤال السابع : ()r () r ولمعرفة مجاالت التزا د والتنالص لاللتران نبحث ف اشارة () r أي أن () r غ ر موجودة غ ر موجودة اشارة متنالص ف () r 9
30 السؤال االول : أ( تمار ن )-( الم م المصوى صفحة 8 ()r () r أك (()r ) ()r ()r ( )r الحل: صفخ الشقاط الحخجة ىي ()r ب( 8 8 () r () r الشقط الحخجة ىي )66( 8-( ) 8( ) الدؤاؿ الثاني : أ( 9 ()r ح () r 8 () r 8 6 الحل: صفخ + + اشارة أي أف : س= أك س= 5 القيؼ القرؾى السحمية لالقت اخف ؽ)س( ىي : ؽ) 5 (= =8+6-8=56 قيسة عغسى محمية ؽ) 6=96+-6= =) قيسة صغخى محمية
31 () r ب( ()r السجاؿ () r صفخ () r س= صفخ ()r ( )r = صفخ قيسة صغخى محمية قيسة عغسى محمية ()r p ()r p () r ج( الحل: اشارة () r القيؼ القرؾى السحمية لالقت اخف ؽ)س( ىي قيسة عغسى محمية + + اشارة ( )r قيسة صغخى محمية ()r () r () r ()r ()r د( الحل: () r صفخ= () r القيؼ القرؾى السحمية لالقت اخف ؽ)س( ىي قيسة صغخى محمية ( )r ()r ()r ىػ( الحل: اشارة اشارة + +
32 () r () r () r أك القيؼ القرؾى السحمية لالقت اخف ؽ)س( ىي : قيسة عغسى محمية قيسة عغسى محمية قيسة صغخى محمية ؽ) 6 ( = ( )r ( )r p ()r () r اشارة ك( الحل: () r ؽ) 5 ( = قيسة عغسى محمية الدؤاؿ الثالث: أ( ()r 8 r r r الحل: إذف ؽ مترل في ]6 ] غيخ مؾجؾدة عشج س= 6 5 تخفض 6= () r () r () r عشجما عشجما تخفض القيؼ القرؾى السحمية ؽ) 6 ( = صفخ ؽ) 5 ( = 8 ؽ) ( = ؽ) 6 ( = صفخ قيسة صغخى مظمقة )اصغخ قيسة ) ؽ) =) قيسة عغسى مظمقة )اكبخ قيسة(
33 ق ب( ()r الحل: ؽ مترل ( حاصل طخح مترميؽ ) () r ؽ) ( = ق - 6 ؽ) ( = القيؼ القرؾى السحمية ؽ) 6 ( = ؽ) ( = صفخ قيسة صغخى مظمقة )اصغخ قيسة ) ؽ) (= ق - ق قيسة عغسى مظمقة )اكبخ قيسة( حدب نغخية القيؼ القرؾى ج( ) ( = ؽ مترل )حاصل طخح مترميؽ ) ( ) ( ) _ عغسى مظمقة عغسى مظمقة صغخى مظمقة ( ) ( ) ( ) الدؤاؿ ال اخبع : 9 f H ()r ؽ) ( عغسى محمية ؽ) ( صغخى محمية () r () r الحل: لالقت اخف نقط حخجة عشج س= س= 9 f H () r 9صفخ f H 9 f H () r f H () r 9 f6 H7
34 كبحل السعادلتيؽ )( )5( نحرل عمى: f H9 6 f H 6H6 () r الدؤاؿ الخامذ: الحل: 9 ()r مترل عمى ح النو كثيخ حجكد () r صفخ = ؽ) ( قيسة عغسى محمية كىي مظمقة النيا كحيجة ؽ) ( = = = إذف )r )سالب p ()r دائسا اشارة تمار ن )-( التمعر ونمط االنعطاف صفحة 87 () r السؤال األول : () r ()r ه : أ( مجاالت التمعر لاللتران ممعرا الى اعلى ف كذلن ف اشارة ()r وممعرا الى اسفل ف كذلن ف () r () r () r ب( ممعر الى اسفل ف كذلن ف اشارة ()r ()r () r ج( اشارة () r () r
35 ممعر الى اسفل ف و ممعر الى اعلى ف ()r () r () r هو ()r مجال ( ) ()r د( اشارة مؾجبة دائسا ( ) () r ( ) ( ) () r ()r ك () r ومنها ممعر الى اعلى ف () r () r ه( ()r () r () r ()r او ترفض ف كون ممعر الى اسفل اشارة ف () r و( ()r اشارة () r () r () r ()r ممعر الى اسفل ف و ممعر الى اعلى ف ()r 5 ()r 5 ز( 5
36 ()r ()r 7 ()r ()r غ ر متصل عند س= ومنها فان r ( )غ ر موجودة اشارة () r غ ر موجودة صفر 5 5 () r () r () r التران ثابت ف و ممعر الى اعلى ف5 ()r p ()r السؤال الثان : أ ) متصل على النه كث ر حدود () r () r () r نمطة انعطاف الن االلتران متصل عندها و غ ر من مجال تمعره اشارة () r ()r اشارة () r ( )r ( )r ب( ()r متصل ف () r () r () r نقاط االنعظاؼ ىي : ألن االلتران متصل عندها و غ ر من اتجاه تمعره. () r () r 5 ()r ج( اشارة 6
37 5 5 () r () r اذن وجد نمطة انعطاف عندما س = 5 الن ق متصل و غ ر من مجال تمعره وه ) ( السؤال الثالث : 6 () r () r ()r أ( () r ()r ل مة صغرى محل ة () r ( )r ( ) r ل مة عظمى محل ة p ب( ()r متصل على () r (6 ) r 6 6 غ ر موجودة اذن غ ر موجودة اشارة () r (6 ) r فشل اختبار المشتمة الثان ة 6) )r ومنها فإن ل مة صغرى محل ة وه صغرى مطلمة السؤال الرابع: ( ) r له عند س= - نمطة انعطاف h ()r h () r 6 h ( ) r 6 h () r h 6 h 7
38 السؤال الخامس: () r (6) r () r أ( من اشارة () r ممعر إلى أسفل ف وممعر إلى اعلى ف اشارة ()r وجد نمطة انعطاف عندما س= الن ق متصل )المشتمة موجودة ). و غ ر من مجال تمعره ه ) ) )) () r اشارة () r ب( ج( ل مة عظمى محل ة r r () r 6 ل مة صغرى محل ة r 6 r (6) r متزا د ف ف ومتنالص ()r وأ ضا ف السؤال السادس: المعط ات: p ] [ f h ] [ f h ()r منحنى ق مر بالنمطة ) 5( ق) 5=) ( ) نمطة انعطاف ق) =) r () r معادلة المماس عند ) ( ه س+ص= 7 الحل: ] [ f h 5 ] [ f h ()r ] [ f h8 ] [ f h8 ()r [ f h () r [ f h [ f h () r f h6 () r f h6 f h () r بحل نظام المعادالت نحصل على 5 ] [6 f h إذن ()r 8
39 r () r r ; ()r السؤال السابع : المعط ات: ) ( نمطة انعطاف افم لاللتران ق)س( ع ع ; احسب الحل: 5 ; ; ; ()r ; () r 8 ; ; 8 ; () r ; () r ; ; ; () r ( ) r () r ع ; ع; ; ع ; ; ; ; ; ; ع 8=8+= )8(+ 5 = السؤال الثامن: المعط ات: ق) =) أ( ل م س الت كون لاللتران عندها ل مة لصوى ه س= س=- بح ث ق) ( ل مة صغرى محل ة و ق)- ( ل مة عظمى محل ة ( ظهر ذلن من خالل اختبار المشتمة الثان ة ) اما ق)- ( ل مة صغرى محل ة ق) ( ل مة عظمى محل ة ) ظهر ذلن من خالل إشارة المشتمة االول الن اختبار المشتمة الثان ة فشل ( اشارة () r ب( لاللتران نمطة انعطاف عند س= ه )( ق متصل عندها و غ ر من مجال تمعره - - ج( ق)س( متزا د كذلن ف ومتنالص ف / اشارة ق )س( 9
40 تمار ن )5-( تطب مات الم م المصوى صفحة 9 السؤال األول : الحل : مح ط المستط ل = الطول ن + العرض ن =8 س+ ص =س+ص ومنها ص= س- مساحة المستط ل = الطول العرض م= س ص م= س) س( >س> م= س- س ] م ] صفر = - س ومنها س= م ] ] م ] ] إذن المساحة أكبر ما مكن عندما س= م ومنها ص= م ومنها مساحة اكبر حد مة متر مربع السؤال الثان : ص س الحجم = مساحة الماعدة االرتفاع ع 9 ع ع 9 المساحة الكل ة = المساحة الجانب ة + مساحة الماعدة )ألنها مفتوحة من أعلى ) م ع+ التكلفة j لu + ل بفرض أن اسم نك من الجوانب كل ف ل إذن اسم من الماعدة 8 ل + ل كلف ل j ل ل + u + ل 9 jل ل + ل j ل + ] ت ل ]
41 8 ومنها نتج أن ل = ل ل 8 ل + سم + ل 768 ل + ل ] ت ل ] 8 ] ت ل التكلفة ألل ما مكن عندما نك= سم ] سم 9 9 ع 6 إذن ابعاد االسطوانة االلل تكلفة ه نصف لطر الماعدة= سم وارتفاعها سم السؤال الثالث : ص ()r ف w ( ) w ( ) ( ) ف [ف ( ) ] t ف ف و w [ف ] [ف ] المسافة الل ما مكن عندما السؤال الرابع : [ف ] اشارة f فh - فف ف السرعة المتوسطة =
42 ص- f+ h f h h f f h [ف ] ع f h ع سرعة الجسم الل ما مكن عند ع F h ع f h ع f ع h f h f h f h نعوض ل مة h من ف f f f f h h h f السؤال الخامس: ص س ف w ف k w w] k ] k] k] ف [ف ] ف
43 6 [ف ] ف 56 [ف ] ف 6 6 [ف. ساعة = ساعة و 5 5 ] المسافة ب ن الباخرت ن الل ما مكن الساعة الواحدة و دل مة دل مة السؤال السادس: حجم االسطوانة = من تشابه المثلثات ومنها ع ع ع ع p p 9 p] ] ومنها ترفض أو 8 8 إذن الحجم أكبر ما مكن عندما ف كون أكبر حجم= ع 8 p] اشارة ] 8 8 سم سم السؤال السابع : 6 سم مساحة شبه المنحرف ) ( س ع س 6 سم ( ) = l ( ) = l
44 / اشارة م _ = ( )( ) l عندما س= وجد ل مة عظمى وتكون اكبر مساحة ممكنة وحدة مساحة fl السؤال الثامن : نفرض lh سم ف كون أ سم د م س سم 8 سم (( ) ) l ( ) l سم ومنها س= = ( ) l وجد عندما س= ل مة عظمى تجعل مساحة المثلث اكبر ما مكن ب ن ج تمار ن عامة ( الوحدة الثان ة ) صفحة 9 السؤال األول: رلم الفمرة رمز اإلجابة أ ج ج د ج أ د ا ج د ب ب ب ج لسؤال الثان : () r () r ( ) نالحظ ان ) ( اشارة ومنها ق)س( متزا د على
45 السؤال الثالث: () r ()r () r () r () r و ق متزا د ف الفترة ومتنالص ف اشارة () ل مة صغرى محل ة ل مة عظمى محل ة ( -) hr ( )r اشارة () r h h h السؤال الرابع : حمك رول أوجد h ()r ق حمك رول ومنها ق متصل ولابل لالشتماق على و h h ( )r h h h h h (h)r h h h h r ( )r ومن )تهمل( السؤال الخامس : ()r 9 6 () r أ( النمط الحرجة عند س= ق)- (= 8- = = ق)- ( = = ق) (= =5+7-7=- ل مة صغرى مطلمة ق) 6 (= =5+5-8 =5-=59 ل مة عظمى مطلمة 5
46 () r وممعر الى اعلى ف r ب( ق ممعر الى اسفل ف ج( ) -6( نمطة انعطاف متصل و غ ر من تمعره اشارة - 6 () r ظل زاو ة االنعطاف = السؤال السادس: أ( اشارة r منحنى ق)س( ممعر الى اعلى ف كذلن ف وممعر الى اسفل ف ب( لاللتران نماط انعطاف عند س= - س= الن ق متصل و غ ر من مجال تمعره السؤال السابع: ق كث ر حدود معرف على 6 مع منحناه ف الربع االول ومنها ق< ف 6 6 ف ق متنالص على مجاله ومنها r ه)س( =- س ومنها ه < صفر ف 6 6 ب ن أن ن = ق ه متنالص ف 6 ف r r r موجب سالب سالب سالب= سالب اشارة r إذن ق ه متنالص ف 6 السؤال الثامن: نك +)ع- ( = ومنها نك =- )ع - ع+ ( اذن نك = ع ع u u u u p u u p u u u u p] u] ع - ترفض أو u سم u نك u6 p ] u] 6
47 fh > ف r r p ] u u] 6 u سم إذن الحجم اكبر ما مكن عندما السؤال التاسع: ()r اثبت أن )ق+ه()س( متزا د ف () r () r ألن إذن ق+ه متزا د ف fh fh السؤال العاشر: r ب ن أن التران متزا د على ق< ه < معان ف الربع االول () r > ف ق متزا د ف fh ه متنالص ف ومنها ق ممعر الى أعلى ومنها fh ف < fh h f r r r r اشارة موجب fh r إذن متزا د 7
48 l السؤال الحادي عشر : ] [ f h ()r ()r [ f h () r h () r f h6 r f f r ()r ] F 8 ()r 8 h () r وبحل المعادلت ن نتج ان ()r السؤال الثان عشر : س مح ط الدائرة = = مح ط الشكل = w w w w مساحة المستط ل = w w l l l l] l] ] ] المساحة اكبر ما مكن عندما l ] االبعاد الت تجعل مساحة المستط ل اكبر ما مكن ه l و عرض المستط ل = طول المستط ل = ص 8
49 السؤال الثالث عشر: مح ط المثلث األول ومنه طول الضلع = مساحة المثلث األول مح ط المثلث الثان ومنه طول الضلع = مساحة المثلث األول ) ( م= مجموع مساحت هما ) ( ( ) l l م س= 9 ل مة صغرى محل ة l مح ط المثلث األول = 9 سم ومح ط المثلث الثان = 9 سم وبالتال طول ضلع كل من المثلث ن = سم كىي مؽ الختبة / السرفؾفات 6 ( صفحة حمؾؿ الؾحجة الثالثة ( الدؤاؿ األكؿ: تساريؽ H أ ) لتكؽ مرفؾفة االنتاج ىي مجسؾع مجخالت العسؾد الثاني يسثل انتاج فخع طؾلكخ 7 ( ) H ب ) الدؤاؿ الثاني: كمشو مؽ الختبة 6 h h فإف = فإف : 5 ككحلػ ( السرفؾفة 7 ( h) )5 ( بسا أف الدؤاؿ الثالث: بسا أف 5 كمشيا فقط أي كمشو. 9
50 مجخالتيا عمى مخبع ة مؽ الختبة 5 فتكؾف الدؤاؿ ال اخبع نفخض السرفؾفة f مرفؾفة F الشحؾ d h أي أف d الدؤاؿ الخامذ: فتكؾف السرفؾفة ب مؽ الختبة 5 كمجخالتيا عمى لجسيع قيؼ ي ىػ 5 H 5 6 d الشحؾdh f 6 5 f 5 تجريبات صفحة 68: التجريب األكؿ: أ( H f f H L9 9 ] [ 9 5 ب ) التجريب الثاني: 5 l 5 5 l 5 كمشيا أي أف 5
51 التجريب الثالث: 5, I, I H فيكؾف G U G U 5 G U 5 أي أف H, I نفخض اف كمشيا 9 w w w 5 6 w التجريب ال اخبع: كمشيا التجريب الخامذ: أي أف 5 w 5 8 كبحل السعادلتيؽ يشتج أي أف )5 صفحة w w 6 w 6 6 w تساريؽ ) الدؤاؿ األكؿ: أ( ب 5 الدؤاؿ الثاني: أ( 5 ب( ب H ب = 5
52 ب( جػ. ب = ج( = H الدؤاؿ الثالث: 6 w w w 6 w w w مؽ تداكي مرفؾفتيؽ يشتج أف: الدؤاؿ ال اخبع: (f H)(f H) f H 6 w إذا كانت f H فبيؽ أف: )( f 6 5 f H الدؤاؿ الخامذ: الحل: H 5
53 )5(----- (f H)(f H) 7 5 f H مؽ )( )5( يشتج أف: (f H)(f H) f H f الدؤاؿ الدادس: اذا كانت H 5 فإف س = كبالتالي س = أك س + =5 كمشيا س = بالتعؾيض ال تؾجج أي قيسة لػ س تحقق أف: مجسؾعة الحل= [ f H ء w w w w w الدؤاؿ الدابع: أ ) نفخض ]f ] h كمشيا w w كمؽ تداكي مرفؾفتيؽ: w w كبحل السعادلتيؽ بالجسع يشتج أف: 5 ص= ص= 5 5
54 ء كبالتعؾيض س= - كمشيا [ [ م ب ) تساريؽ ( ) صفحة 9 5 ()5 l 5 l5 الدؤاؿ األكؿ :جج قيسة كل مؽ السحجدات اآلتية : = = 6+ 5 حػ( 8 ب ) أ (: الدؤاؿ الثاني : بسا أف
55 ص 5 6 h 5 h 9 h الدؤاؿ الثالث f h fh f f f 5 h f5 h : إذا كانت h ككاف 5 h فسا قيسة/ قيؼ س = 9= كمشيا س 5 5 h 5 h الدؤاؿ ال اخبع الحل: 5 h أي أف 5 h الدؤاؿ الخامذ : لسعخفة نقؾ بايجاد السحجد عؽ طخيق مجخالت معادلة السدتقيؼ السار بالشقظتيؽ 5( ) 5(.) 7 العسؾد الثالث: w w w w w5 7 w 5 +ص 5 - w w w 5 أ( أ( أك الدؤاؿ الدادس : ضخب الرف األكؿ في )-5( كإضافتو لمرف الثاني أي 5 55
56 6 5 5 ب( إخ اخج عامل مذتخؾ مؽ كل مؽ الرفيؽ األكؿ كالثاني فتتداكى السجخالت الستشاعخة في الرفيؽ فتربح قيستو صف اخ ج( )تبجيل عسؾد مكاف عسؾد فإف قيسة السحجد تزخب بػ )-(( الدؤاؿ الدابع : h [ f [ f h أ( f [ h بجسع العسؾديؽ األكؿ كالثاني h h [ f ع +ع [ f h [ كبأخح )أ + ب + جػ( عامل مذتخؾ مؽ ع يشتج أف: f f [ h h [ ألف بو ع =ع f 5 9 ب( بسا أف السرفؾفة ىي مرفؾفة مثمثية عمؾية فإف محجدىا يداكي حاصل ضخب 5 السجخالت عمى القظخ الخئيدي = 56
57 ) صفحة 55 تساريؽ) - 8 h ليا نغيخ ضخبي. : 8 h 6 الدؤاؿ األكؿ ليا نغيخ ضخبي. ليذ ليا نغيخ ضخبي. f 9 9 [ f [ 9 6 ] ] ليذ ليا نغيخ ضخبي. ; f ; ; ; ; ; ; h f ; ; الدؤاؿ الثاني: بسا أف أ مرفؾفة مشفخدة اذف محجدىا يداكي صف اخ. ; ; ; ; h ; ; ; ; كبسا أف ب مرفؾفة مشفخدة اذف محجدىا يداكي صف اخ. 5 h 5 5 H الدؤاؿ الثالث: 57
58 H H h 5 5 H ( H) الدؤاؿ ال اخبع : h 5 5 h 5 h h 6 = 5 س = 5 س = 5 h w H H H H h h h h h w h h w h س الدؤاؿ الخامذ: بسا أف: لكؽ بسا أف: إما إذف w w w أك w. f [h الدؤاؿ الدادس : f h h الحل: h f h] أ غيخ مشفخدة 58
59 f h [h f [ f h h h [ l f f h [ h h f [ w g. h) ; (h;) ; ; كمشيا h; ;ع ; ( H ; الدؤاؿ الدابع : لثبات أف : w g h ع نفخض أف: w g ; h; ع w g w; g; u H; ; u; H ; (H;) h w g ( H) ( ) ; u H ; [h fh [h h fh h [h fh [ f [ lf l الدؤاؿ الثامؽ :بسا أف بما أنH غيخ مشفخدة فإف مؾجؾدة )5 صفحة تساريؽ ) الدؤاؿ األكؿ w 6 w 6 w أ( 59
60 h h 9 6 w كمشيا س= ص = 6 5 h ب w) w w 9 9 H فتكؾف 9 H w كمشو w w الدؤاؿ الثاني : س أ( 5 w w 5 5 h h h ص h h ص ص - hس h س 6
61 ب ) w w wh Hس w H wh w H H 5 : H Hس H س الدؤاؿ الثالث 5 Hص 5 Hس H wh w H H H س 5w w الدؤاؿ ال اخبع : كنجخي العسميات عمى الشحؾ اآلتي: السرفؾفة السستجة لمشغا ىي H w 5 w w w 7 كبالتعؾيض العكدي ( ) س = كمشيا تكؾف w أ( 6
62 u w u w ب( 6 u w 6 كنجخي العسميات اآلتية: نكؾف السرفؾفة السستجةH 6 6 ww ww 6 9 ww 6 w كمشيا - كمشيا ع= ع=- 9 كبالتعؾيض العكدي: ص=- 6= س+ + كمشيا س =5 تساريؽ عامة) الؾحجة ) صفحة 5 الثالثة الدؤاؿ األكؿ ( السؾضؾعي( رقؼ الفقخة رمد الجابة أ ء ب ء ب أ ء جػ جػ جػ فإف 7 w w الدؤاؿ الثاني: بسا أف 6
63 7 w 7 w w 7 w 7 كبحل السعادلتيؽ معا يشتج أف: س= 5 ص= 5 الدؤاؿ الثالث : h h 5 h 5 5 hh أ ) 8 9 h 9 h ب ) 5 5 h 9. جػ( ) (h الدؤاؿ ال اخبع : ليجاد قيؼ س التي تجعل فإف : إذف 9- = 9-6
64 w كىحا يعشي أف: س ىي أي عجد حقيقي. الدؤاؿ الخامذ : أ( لحل السعادلة السرفؾفية )باستخجا الشغيخ الزخبي( 6 h فإف : h 5 w كمشيا س= -5 ص = ب( لحل السعادلة السرفؾفية w فإف: 9 w 8 w8 9 w س = w ص = w 6
65 w 5 h h 5 الدؤاؿ الدادس : hh w 5 w 6 w5 5 5 بسا أف: كمشيا س 5 = س = 5 ص + 6 = ص = -, fh الدؤاؿ الدابع : f h نفخض أف : كال مؽ السرفؾفتيؽ ليا نغيخ ضخبي كليكؽ,, H (fh) H, fh بسا أف :, H, fl f(h H), f, f(fh) أي أف كسا أف كندتشتج أف كىحا يشاقض الفخض بأف إحجى السرفؾفتيؽ عمى األقل مشفخدة. الدؤاؿ الثامؽ : 5 k ; w H 5 H k h ; أ ) H كمشيا ; 6 k h h ص 8 ص 8 hس 8 8 h ب ) س 65
66 الدؤاؿ التاسع : h H ( h) = ( أالحظ أف: (h 8 8 ( h) H 8 h h 5 ص + س = 5 ص= - الدؤاؿ العاشخ : لحل السعادلتيؽ بظخيقة كخيسخ : س+ ) نختب أكال( 5 hس 6 س - h h h ص ص hس 5 h h 9 ص h : الدؤاؿ الحادي عذخ : الشغا اآلتي لحل بظخيقة جاكس u w u w 9 u w نكؾف السرفؾفة اؿ 9 مستجةH كنجخي العسميات اآلتية: 66
67 ww w w w w w 5 5 ww 5 5 ص = ع = 5 كمشيا ع = كمشيا 6 كبالتعؾيض العكدي: ص + ع = 5 س = 9 5 ع = 5 س+ 5 9 الدؤاؿ الثاني عذخ : حدب خرائص السحجدات فإف محجد السرفؾفة القظخية العمؾية يداكي حاصل ضخب مجخالت القظخ الخئيدي أي أف ومنها أي أن 67
68 اجابات الفصل الثان الفرع العلم والصناع 68
69 5 الدؤاؿ االكؿ ا( حمؾؿ الؾحجة ال اخبعة تساريؽ كمدائل )-( صفحة ()r ( ) ()l ()r () ( ) () l أي أف ()l اقت اخف أصمي لالقت اخف ()r ()r ب( ()l ()r () l أي أف ()l ليذ اقت اخنا أصميا لالقت اخف ()r ج( ()l ()r ()r () l أي أف ()l اقت اخف أصمي لالقت اخف ()r الدؤاؿ الثاني: بما أن)l ) () التران ن أصل ن فإن()l [ ()I كمشيا [ ()I ()l 7 6 ()I 7 ( )I الدؤاؿ الثالث: 77 () () l () l ألف 7 ()r () () l حيث ()r مترل عشج س = 69
70 الدؤاؿ ال اخبع: بسا أف)l ) ىؾ احج االقت اخنات األصمية لالقتخ اف السترل ()r فإف ()r () l ( ) () l ( ) ( ) ( ) ( ) ( )r )وم ) ( ) ( ) ( )( ) نها كون h الدؤاؿ الخامذ: [ h R وباشتماق الطرف ن نتج [ h ] R )(... [ h بما أن R فإن )(... فإن h وبما أن R h6 كذلن R [ وبحل المعادلت ن نتج أن h 6 الدؤاؿ األكؿ تساريؽ كمدائل )5-( صفحة [ 8 ]8 ]( 7) ]( 7) [ 7 5 [ ]( ) ] ( ) 5 [ 5 ] 5 أ ) ب ) ) د ) ج ( )( ) ] ] ق( 5 [ 5 7
71 [ 5 ]( 5 ) ] 5 ك ) [ ] ] ز ) [ 5 ]( 5) ]( 5) ح ) الدؤاؿ الثاني: ] ]( () r) [ ()r ()r بتكامل الظخفيؽ كمشيا [ ()r كبسا أف فإف أي أف [ كمشيا ()r الدؤاؿ الثالث: ]()r كباشتقاؽ الظخفيؽ يشتج أف: () r كمشيا ()r ( كىؾ السظمؾب. ) ( ) ( ) r ( )r الدؤاؿ ال اخبع: بسا أف r) [ ] ( () فإف [ [ ()r [ [ 5 ()r [ 5 () r [ كمشيا [ 5 () r [ 5 ()r 6 [ كمشيا [ لكؽ ()r ( )r 6 5 فيكؾف ()r 7
72 كمشيا [ ( ميل () r h 5 [ 8 5 -( صفحة ( الدؤاؿ األكؿ: ميل السساس = كمدائل تساريؽ ( ) () r كمشيا 5 ()r فيكؾف ]( ) ]() r لكؽ [ ()r فيربح ()r الدؤاؿ الثاني: بسا أف wىؾ = مساس لسشحشى السساس( أي أف كمشيا )r )عشجما س = فإف فيربح () R كمشيا [ ()R ()R h [ h ()r ()r h h ]( ) () R لكؽ نقظة التساس ىي ( الدؤاؿ الثالث: ميل السساس كمشيا h () r ] h ]() r كمشيا [ كبسا أف ()r فيربح فإف كسا أف فإف أي أف () r ()r الدؤاؿ ال اخبع: [ ] ]() r () r كبسا أف ( ) r فإف [ كسا أف كتربح ] ]( ]() r ()r لكؽ ( )r فيكؾف ] ( )r كمشيا ] ()r فيكؾف 7
73 أف k] k u] كمشيا الدؤاؿ الخامذ: k u] k] j [ أي أف [ k u كبسا أف سخعتو االبتجائية مقجارىا / ث فإف 5 فيكؾف k u كيكؾ ف (5)u )[k كبتكامل الظخفيؽ يشتج: k ) t] كمشيا k t] كسا أف k] u k k t فيكؾف ()t كبسا أف ] k k t (5)t مت اخ 6 6 الدؤاؿ الدادس: k]( 5k) كيشتج p] نفخض حجؼ الؾعاء p فيكؾف k] 5k p] كمشيا k5 k p [ k5 k p كبسا أنو فارغ فإف p() k5 يكؾف k فيكؾف كبحل السعادلة يشتج أف كلسعخفة الدمؽ الالز لسلء الؾعاء فإف : ثانية. ( ) k أي أف الؾعاء يستمئ بعج 56 ثانية. () r الدؤاؿ الدابع: ميل السساس كمشيا ] ]() r [ ()r كيشتج أف فيكؾف كبسا أنو يسخ بالشقظة ()r أي أف [ [ 7
74 k t] k] u الدؤاؿ الثامؽ: نفخضt : ا ازحة الجدؼ عؽ قسة البخج فيكؾف كمشيا ()t 5t لكؽ k](k ) t] [ k k5 t k k5 t أي أف فيكؾف كعشجما فإف الجدؼ يرل األرض كمشيا 9 ثانية k 5 k كمشيا k5 5 k k5 t أي أف الدؤاؿ التاسع: w](w) [ كمشيا يكؾف ] w]( w) ] w]( w) ] أي أف w) )[w كمشيا [ فيشتج w w لكؽ عشجما w فإف [ كنجج ص بإكساؿ السخبع في ص فيكؾف w w w] ( ) ] 56 -( أ( ب( تساريؽ أ( صفحة الدؤاؿ االكؿ: [ ( ) ] 5 ( ) ] 5( ) ]( ) w] ] ( ) نفخض w فيكؾف كمشيا w] w ( ) ] ( ) ( ) [ [ w w]w ] ج( ] w] أي أف ] w] كمشيا نفخض w ( ) w w [ [ w] ] 7
75 5 ] w] ] ( w د( نفخض فيكؾف كيكؾف w]( w w w) w] w( w w) ] ( [ ( ) ( ) ( ) [ w w w ىػ( ] ( ) نفخض w فيكؾف w] ] 6 6 w] w w ] ( ) [ w9 w6 w w]( w9 w6 w) ( )9 ( )6 ( ) [ ] ( ] ك( ]( ) ] ( ) ]( ) ]( ) 8 8 [ ]( ) ] ] ( )( ) ز( ]( ) ] ] ( ) [ ( ) ] ] ( ) ح( ( ) ( ) [ ( ) ] ] ( ) ( ) 75
76 الدؤاؿ الثاني: ] أ( ] 5 ] w] نفخض w فيكؾف w]( ) w ] كمشيا [ ( ) [ w w] w ] ب( نفخض فيكؾ ف ] w] w [ [ w w]w w] w ] [ ] ] ] ]( لكؽ ] 5 [ ] 5 ( ) 5 ( ) 5 5 ( ) ( ) د( ] ] ] ] 5 7 نفخض w كمشيا يكؾ ف ] w] 5 5 ( ) 5 ( ) w] w ] ] 7 أي أف [ ( ) [ w w] w 7 ىػ( ] ( ) ] (( ) ) ] ( ) ] w] نفخض w فيكؾف ج( [ ( ) ] w 6 7 كمشيا ] ( ) ] ( ) 76
77 ك( ] ] ]( ] ] ] w] نفخض w كمشيا فيكؾف [ w ] w]w ] ] ] [ ) صفحة 66 تساريؽ ) ب الدؤاؿ االكؿ: ] أ ) ] u] u أف: r ] r] نفخض [ ] ] ] ب ) ] u] r نف ضخ أف: u ] r] [ ] ] ] ] ] u] ( ) نفخض أف: r ] u r] ] ] ج( 77
78 ]( 6 6 ] 6 ] [ 6 ] ] u] نفخض أف: r u ] r] [ ] ] د ) ] ] ىػ ) ] w] كمشيا نكامل بالتعؾيض بفخض أف w w] w ] ] w w] ( w) كىشا نكامل باألج ادء w نفخض أف: w] u] ( w) r w w] u r] w w [ [ ( w) ] ] ك ) w]w u] w u ] كمشيا w]w S w w]w w ] نفخض أف: نفخض ثؼ نكامل باألج ادء w r w] r] 78
79 [ w w w w]w w ] [ S S S 79 ] ( ) I ] ( ) I ] ( ) u] نفخض أف: r u ]( ) r] ( ) ] ] ( ) I ] I ( ) ( ) ] () [ ] ] ] ح( ] u] ن فخض أف: r u ] r] ] ] ] ] ثؼ نكامل باألج ادء مخة أخخى لمسقجار ] u] ن فخض أف: r u ] r] ] ] ] 8 8 [ ومنها ] 5 5 ] ] ] ) ط( ] u] r ] r] ز( أف: نفخض
80 ] ] ] ) u ] ] [ ] ) [ ] ] ي( كمشيا نفخض w w]w w ] ] w] ثؼ نكامل الشاتج باألج ادء فيكؾف الجؾاب الدؤاؿ الثاني: k ] u] نفخض أف: r k u ] r] k k k k ] ] k k k k k [ ( ) k k ( k) k 65 8 تساريؽ )- ج( صفحة الدؤاؿ األكؿ: ] ] ( )( ) أ( f H ( )f ( )H كمشيا يكؾف ( )( ) f 5 كتكؾف H كمشيا 5 [ ] ] ] 5 ( )( )
81 . [ بسا أف درجة البدط تداكي درجة السقا ب ) 6 6 كيشتج أف فشجخي القدسة السظؾلة 8 ( )( ) 6 6 f كبعج الحل يشتج أف H F h كمشيا ( )( ) [ 6 I I ] كيكؾف ] كمشيا w]w w نفخض ] ج( [w w كبإج اخء القدسة السظؾلة يشتج أف: ] w w f H w w w w w w w w [ ( 8 ( ] ] د( ( )( ) [ f H [ f H كيشتج أف ( )( ) [ ] ( )( ) ( ) ] ] [ ( ] ىػ ) 8
82 ] ك ) I ] w] كمشيا الحل: نفخض w w] w] w] w w w كمشيا f H w w w [ ] I I I ] 7 ز ) f H f H كمشيا 7 ( )( ) [ 7 ] كيشتج أف ] w] ] نفخض w كمشيا ح ) 6 w] w] ] 6 w w 6 6 f f H كمشيا H 8 8 w w 6 w [ w 8 w ] 8 6 [ أي أف ] ] w] نفخض w ] ] ط( كمشيا ثؼ نكامل بالكدؾر الجدئية w] w] w w ] 8
83 ف كيشتج أف f H فيكؾ F h [ ] ] I I w w ] ] ] w w w ] ( ) ( ) 6 (d w] ( w)w ] 6 ] w] نفخض w كمشيا فيكؾف [ ( I I ) ] 6 كيشتج أف الدؤاؿ الثاني: كمشيا بسا أف w] ]6 w] فإف w] ] ( ) 6 S U كنفخض ] w أي أف ] w] ( ) 6 ( ) 6 U]( U) [ U I U w فيشتج أف U) [ U]( أي أف U 6 [ S I 6 كيشتج أف ( S) w [ 5 كعشجما w فإف [ () كمشيا 5 I ( ) w S S 6 8
84 66 5 (: صفحة الدؤاؿ األكؿ: الفقخة السؾضؾعي تساريؽ عامة)الؾحجة ال اخبعة 5 ج االجابة الدؤاؿ الثاني: د ج ب يكؾف)l ) اقت اخنا أصميا لالقت اخف ()r اذا كاف ()r () l ()R كبسا أف () l الدؤاؿ الثالث: كمشيا ب 6 [ فتكؾف () r [ () R ]( ) ]() r [ () r كبسا أف 6 () r ] 6 ]() r ()r 6 ()r [ كمشيا ()r أي أف كسا أف كبسا أف الدؤاؿ ال اخبع فإف K]( K) I K) K]U (K)T [ ( K) K ( K) K K (K)T I فيكؾف كبسا أف 8 ()T فإف [ 7 7 ( K) K ( K) K K (K)T I I I ()T مت اخ الدؤاؿ الخامذ: ] w] w] ] بسا أف فإف 8
85 ] U] ( ) U نفخض فيكؾف كمشيا يكؾف [ U] U] w U6 ( ) U 7 w 8 ( )6 [ w ( )6 س = أي أف كعشجما ص= الدؤاؿ الدادس: يكؾف ] w] [ ( ) نفخض w فيكؾف ] فيكؾف w] w 9 ] w] 8 فيكؾف w نفخض ] 9 ] )5 9 ( ) w] ] 9 ] أي أف ( w)w 9 ( ) 9 9 [ ( I I كبالكدؾر الجدئية يشتج أف: [ ) 9 ) ]S نفخض S w فيكؾف ] w]w أي أف ثؼ نكامل باألج ادء ) w]w w ]S w]w u] w r أف: w u w] r] w]w w w w]w w ]S [ S I S S [ ] ] نكامل باألج ادء مختيؽ فيشتج أف : ) نفخض 5 [ ] 85
86 ] u] u 86 ( ) r ] r] ]( ) أف: نفخض ] ( ) ]( ) ثؼ نقدؼ كنكامل بالكدؾر الجدئية كيشتج أف: ( )[ [ ( ) [ I ] ] ) 7 ] w] ] نفخض w فيكؾف ) 8 [w w ثؼ نقدؼ كنكامل بالكدؾر الجدئية w] ] w w [ I I كيشتج ] ]( )( ) ]( ) )9 [ ] ] 7 ] 8 )6 8 7 [ ] ] (6 ) ] (6 ) ] (6 ) 8 [ h ( ) [ (6 ) ] (6 ) الدؤاؿ الدابع: K]H T] T] ts كمشيا H فإف ts بسا أف H u t S K] [ KH كيكؾف t K]H T] t كحلػ 6 ()t فيكؾف كمشيا 6 [ h h لكؽ 9 ()t كبحل السعادلتيؽ يشتج أف
87 الدؤاؿ الثامؽ: ] w] فإف ] بسا أف w] كمشيا [ w فشكامل بالتعؾيض بؾضع U U فيشتج أف [U I w كبعج اج اخء التكامل باألج ادء يشتج أف كعشجما ص= 6 فإف: [ w I w الدؤاؿ التاسع: نكامل الظخفيؽ بالشدبة ؿ س ] ]()R ]( R ]( كبتكامل الجدء األكؿ R باألج ادء يشتج أف كمشو كمشيا يكؾف ()R [ ]()R ]()R ( R أي أف()R [ كبسا أف ( )R فإف] ()R حل آخخ: بسا أف ()R ( R فإف (()R) فإف] ] كبسا أف ( )R حلول الوحدة الخامسة تمار ن )-5( صفحة 76 ] (()R) أي أف()R [ (h 6 السؤال األول: الفترة الجزئ ة الرابعة f) 87
88 [ [ [ 7 السؤال الثان : ومنها فتكون 5 ألن طول الفترة الجزئ ة ساوي السؤال الثالث: v ((5) r () r () r () r) ( )r (r )l v v ( 9 ) (r )l السؤال الرابع: ()r طول الفترة الجزئ ة = فتكون 7 v v v (() r () r ( ) r) ( )r (r )l 8 6 H 5 السؤال الخامس: ()r الفترات الجزئ ة ه : 8 66 H6 H H H (r 5 )l f H H H8 5, ومنها كون السؤال السادس: ومنها ومنها h hf 8 ومنها f H وبحل المعادلت ن نتج أن : h hf f ()r 6 h السؤال السابع : (r )l
89 ( ) 6 6 kv ( v )r (r k )l ; k v k السؤال الثامن : طول الفترة الجزئ ة kv ( v)r (r k )l g k v kv kv ( v )r ( v )r ; g v v k ( k)r ( )r ( )r ( )r g k (( k )r ( )r ( )r ( )r) ; k k (()r ()r) ( )r ( )r ; g k k )-5( صفحة 8 H f وبالطرح نتج أن السؤال األول: تمار ن kv v v v ( v )r (r k )l k v k v 7 (v )r ( v ) r k k و كون kv ( ( k)k k7) (v 7) (r k )l k k k k k v k (f ( v ) h) ( v )r (r )l k k k v v k السؤال الثان : k k k v v v f (( v ) )h (f ( ) h k v k k f ( )lh 89
90 f (v k f k k = v k f f k v k السؤال الثالث: ( )r ] ( k)k ( ) ) (v f f f f k k k k k k 5 ( 5) k k = ( f) ( f) ] f باالختصار والتبس ط نتج ان وبحل المعادلة نتج الم مة المطلوبة ب= 6 السؤال الرابع: نستخدم تعر ف التكامل المحدود ( ر مان (و نتج ان k 5 ( )r (r )l v k k v ] (h k k 5 5 k (v )r k v v 5 5 k 5 5 (r k )l ] k k و نتج أن k (v )r k ( v )r k (r k )l k v v k ب( k k k k v k v ((v 6 ) ((v )6 ) k ( k)k 5 (( 6 k ) k k k 5 (r )l ](6 ) k k 9
91 ف كون () ()r ) ()r السؤال الخامس: نفرض الحظ ان معرفا على الفترة () بما ان () حسب النظر ة فان متصال على مجاله فهو لابل للتكامل ا ضا لابل للتكامل على الفترة ()r تمار ن ( ) 5 صفحة 86 = ]( 69) ] ( ) السؤال األول: أ( 76 9 ]( 6 9) بفرض ] ( ) 5 ( ) 8 8 w] (w) = w ( ) ب( واجراء التكامل بالتعو ض نتج ] ( ) ] ج( ] ] r ] r] باألجزاء ( ) I ] 9
92 w] ] w ] ( ) د( بفرض w] (w) ( w) ] ( ) 5 w]( w w w) w] w( w w) ( ) ( ) ( ) ( ) ( ) ف الفترة السؤال الثان : ()r w] w w](w)r ()j w w] w] w] w w w ( w w) 8h ) h ( ومنها السؤال الثالث: ( )j بما أن فإن كما أن ت)س( متصل دائما على مجاله f ومنها f ومنها تكون ( )j ( )j [ w](w)r ()j [ [ ( )j السؤال الرابع : لمعرفة ل مة الثابت ج فإن ومنها 9
93 ()r () j ()r إل جاد r() نعوض بدل س )( ف نتج ان السؤال الخامس: ( h) () j ومنها h 5 ] ( )( ) ( h) () j السؤال السادس : وعندما ف كون w] ] نفرض w س= فإن ص= وعندما س= فإن ص=- 5 5 w] (w)( w) w] (w)( w)( w) أي أن 6 8 w w 5 7 w]( w w) 6 8 تمار ن )-5( صفحة 9 ]( ) ] (h السؤال االول: ( ) ]( ) ] ( ) (f ( ) ( ) ]( ) ]( )( ) ([ ( ) 9
94 (9 )() ] ] د( ( ) ]( ) السؤال الثان : ( ) ()r نفرض أ( ( ) ( ) الحظ ان ()r دائما الن المم ز سالب ومنها ]( ) ]( ) أي ان ( ) ( ) ب( ال حظ ان p و حسب خاص ة الممارنة ]( ) ] ] ] 5 السؤال الثالث: :أ( ] ] ] ] ] ب( 5 ]( ) ] ] ج( 5 5 ]( ) ]( ) ]( ) ] ] ]( ) 5 9
95 ()( ) ] ]( ) ] ]( ) 7 7 د( ]( ) ]( ) ]( ) ]( ) 5 7 ]( ) 7 7 ]() r 5 السؤال الرابع: ] ] ]()r ]( ()r) 8 () 7 (H h 5 5 7h ]()r h ]()rh ب( السؤال الخامس: ومنها 6 ] ] 6 6 ومنها 95
96 8 ]() r 5 السؤال السادس: ] ]()r ]( ()r) (h 6 8 ]( ( )r) 7 ب( 5 7 w](w)r ]( )r بفرض w وتبد ل حدود التكامل صبح ] w](w)r ]( ( )r) السؤال السابع: 7 ]() r5 9 ]() r (]()r ]()r ) ]()r ]()r 7 (]()r ]()r ) ( ) 8 ]() r السؤال الثامن: 8 ] ]( h) ]()r 8 (8 7) ( )h h h 96
97 9 u u] u السؤال التاسع: ف كون f f ](9 ) ](u] u ) (5 f)( f) ومنها 5 f9 f أي أن 5 w](w ) w](w) r ()j w](w) r ]() w](w) r ()j ()r f f السؤال العاشر: عندما عندما فإن فإن ومنها 5 ( ) w]( w) ()j ()j 5 تمار ن ) -5 أ( صفحة ) ) السؤال االول : ] ] ()r l وحدة مساحة 97
98 السؤال الثان : معادلة المستم م w المار بالنمطت ن أ) ( ب) ( ه w w نجد نماط تماطع ق)س( والمستم م س= أو س= - ترفض ] ] ()r l 5 وحدة مساحة السؤال الثالث: 9 ()r ومنها س= أو س= ترفض ألن المساحة ف الربع الثالث س=- س=- ] 9 ] ()r l ] 9 وحدة مساحة
99 السؤال الرابع : نجد نماط التماطع ب ن أوال : ق ص ثان ا : ن ص م = م + م + م ] وحدة مساحة ] ] ] ] وحدة مساحة م م م - ه ] م = م = م + م + م وحدة مساحة السؤال الخامس: نجد نماط التماطع ب ن ; ()r أو س= ترفض م = م + م ] ]()r م وحدة مساحة 99
100 ] ] ; ()r 8 وحدة مساحة م= م وحدة مساحة أو س= السؤال السادس: ()r ; ()r ; م = م + م م ] ] ()r وحدة مساحة م ] ; () وحدة مساحة ] 8 6 م= وحدة مساحة تمار ن ) -5 ب( صفحة 5 السؤال األول: ()r ومحوري الس نات والصادات والمستم م س= 5 حول الس نات 5 5 ]6 ]() r p وحدة حجم الحل : 8 56
101 ()r السؤال الثان : ومحور الس نات والمستم م ن حول ()r 6 ] ]() r p الس نات وحدة حجم الحل : 6 6 السؤال الثالث: معادلة المستم م ج د ه w w w وحدة حجم ] p 6 السؤال الرابع : 5 6 ()r حول الس نات الحل : نجد نماط التماطع ب ن ()r ] () r ] 6 ] وحدة حجم 5 5
102 ومحور الس نات السؤال الخامس: بالتعو ض ()r ] ]() r p w w نفرض أن w ] w] ] w] عندما w w نكامل باألجزاء w ] w p w]w r] w ()r w w, w],] نفرض أن ونفرض أن w w w w] w w] w w p w w] w باألجزاء w w, w],] w] r] w r نجد نفرض أن w w w w] w w] w وحدة حجم p السؤال السادس : الحل: نجد الحجم الناتج من دوران المساحة المحصورة ب ن u دورة كاملة ومحوري االحداث ات والمستم م ()r u حول محور الس نات ] ]() r p uوحدة حجم u u
103 السؤال السابع: ()r ومحور الس نات والمستم م ن س= س= دورة كاملة حول محور الس نات 6 ] ]() r p نكامل بالكسور الجزئ ة الحل : ] 6 6 f h 6 f h 8 f 6 f 8 h 6 h عندما ] 8 ] 8 p 8 8 P ( وحدة حجم ) تمار ن عامة ( الوحدة الخامسة ) صفحة 6 ج 9 ج 8 ب 7 ب 6 ج 5 د أ ج أ ب الرلم رمز االجابة السؤال الثان : )(----- )(----- جدfh f h 7 h f v h v k h f h f f h h 6 h 6 h f h f f h 8 h 7 h
104 f h 8 f h f f h h السؤال الثالث: ()r 6 ()r l v v v v v v v v v v v ( )r ( )r 6 ( )r ()r l r ( ) () l v 6 r 6 v v v v v السؤال الرابع: 5 ()r v v k h f v v k k k ( )r ()r l kk k v v 5 k k k v k v k 6 k k k k k k k 6 6 ()r l ] k ()r ()r 5
105 ()r السؤال الخامس : نمرض أن نجد الم م المصوى () r ومنها تكون ل م س الحرجة ه : س=- ()r ()r ( )r 8 ] ] ]()r ] ()r اذن حل آخر: مكن حل السؤال باستخدام المتبا نات ومنها وبإضافة نتج أن ] ] ] ومنها ف كون 8 ] و نتج أن السؤال السادس : j ]()r 7 8 r j ()r () r 65 () r () r 8 5
106 )( السؤال السابع: ت) =) ومنها +8 ج = إذن ج =- ت)س( متصل عند س= j أ( j 6 f h 8 f h h ف معادلة )( فنحصل على ما ل : j ()r 5 h 8 h j j نعوض ل مة 8 f 6 f j j ]()r ب( السؤال الثامن : نفرض ان w w 5 ] ( ) ( )56 أ( w w ] w] 5 5 w] (w) ( w)56 ] ( ) ( ) w] w( w w)56 w] (w) ( w)56 6 w 8 7 w6 8 w7 w] 5 w56 6 w 7 w56 ],] ] r] r ] ب( نفرض ان ] ] 6
107 5 5 ] 5 ] 5 f f h 5 5 6f f 5 5 h h 5 عندما f ] ] h ] 5 ] 5 h ( )6 ( 5 )5 ] ] ج( ] ] ] د( نكامل بالتعو ض w] نفرض ان ] ] w] w عندما 5w عندما w w] 5 w ] ] 5 5 w w] w 5 ] ] ه( نكامل بالتعو ض ] w] ] w] w نفرض ان 7
108 w] ] ] w w w] w 5 ] السؤال التاسع : وذلن بفرض ان ] w] w ] r ] r 5 7 عندما 5 w 7 وعندما w وذلن بفرض ان ] w] w ] ] 5 عندما 5 w وعندما w 5 5 ] ] r 5 r 5 5 ] ] r ] ] r 5 5 وهو المطلوب ] ] r 7 8
109 عندما r السؤال العاشر : ( نجد نماط تماطع ترفض ] ] م وحدة مساحة عندما ] ] م وحدة مساحة وحدة مساحة م = م + م = r ) r م = م + م +م 6 ] 6 6 م وحدة مساحة 9
110 س ) ] 6 6 م وحدة مساحة ] م وحدة مساحة وحدة مساحة م ) ( 6 السؤال الحادي عشر : f ] h ] ] ] f h ] ] السؤال الثان عشر : r والمماس المرسوم له عند ( ) ومحور الس نات =r المماس م ل r معادلة المماس ه ص- = -( ص= س- م = م + م ] ] r م
111 وحدة مساحة ] ] w ()r وحدة مساحة م وحدة مساحة السؤال الثالث عشر: w r والمحور ن االحداث ن ] ] وحدة مساحة م م السؤال الرابع عشر: أ( ف) 5 ( = بعد الجسم عن النمطة وعندما ن= 5 ثوان 5 5 k] k k] k5 k] k u 5 t م k k5 k عندما ب( ku عندما k k k تولف الجسم عن الحركة عندما ن= k] k k] k5 k] ku t وحدة مسافة
112 السؤال الخامس عشر: r r r w] ] w] ] ] r w] r w w r نفرض ان أ( k k k w] w w] w w ] r k k p [ [ r [ w k k r r r r ب( [ r ] ] r r [ h r r ] السؤال السادس عشر : h ما ل مة ] ] w] w w w w w] w h w] w ] w w نفرض ان عندما h نكامل باالجزاء ] ] نفرض ان ] r] r
113 h ] ] ] ] السؤال السابع عشر: ; ; ; ; ] ] ] ]() ; u] (); u ; ] نكامل الجزء األول باألجزاء نفخض أف: r ] r] ; ; ; ; ; ] ] ] ف كون 6 ; ; ; ] ومنها ; ; r ; r حل آخر: نفرض ان 6 ; ; ; ; r r ] r ] ; 6 ; ; 6 ; ; السؤال الثامن عشر : ومحور الس نات و المستم م ن س= س= w 86 w w w الحل :
114 8 6 w ] 8 6 ] w p ( وحدة حجم السؤال التاسع عشر : w w 6 6 وحدة حجم ] ] p السؤال العشرون : وحدة حجم ] r p p p p ] 7 السؤال الحادي والعشرون : م = ] r معتمدا على الشكل المجاور اوجد علما بأن م =
115 ] w] ] w] w الحل : نفرض ان : وعندما س = فان ص = عندما س = - فان ص = - w] wr w] wr ] r l l w] wr w] wr حمؾؿ الؾحجة الدادسة)األعجاد السخكبة( 55 الدؤاؿ األكؿ: تساريؽ كمدائل )-6( صفحة j ) j 5 j 5 j j )5 8 8 j j j j ) الدؤاؿ الثاني: العجد السخكب الجدء الحقيقي الجدء التخيمي ت M 5 j j9 9 j j6 j6 9 5
116 5-6 6 الدؤاؿ الثالث: البخىاف : الظخؼ األيسؽ : - 5 ت= 6 5 ت j j j j j j j j j ( M) M الدؤاؿ ال اخبع: = الظخؼ األيدخ M j j ( M) j j j ) j ( M) j j j j j j 65 ) j j j j j j 7 j j ) j j j j ( M) j ( M) الدؤاؿ الخامذ: البخىاف : الظخؼ األيسؽ= j j j j j j j j j j j jj = الظخؼ األيدخ 6
117 تساريؽ كمدائل )5-6( صفحة 556 الدؤاؿ األكؿ: أ( j 5 j j6 j5 j68 ب( j5 j j j j5 9 j 9 j 9 ج( j j j j j6 j9 j j69 j j7 j96 j7 j8 j7 j96 د( j5 j j j5 j j j j 5 j j96 j j96 6 ك( j j j j j8 j j j8 j8 j 8 الدؤاؿ الثاني: j 5 j بؾضع jf h j jf h5 jf hj jf h M(F ) F F j Mf h j f5 H5 H5 f h H f f H6 7
118 f5 H f f H H f6 H H H j f h الدؤاؿ الثالث: j j w w j w w j w w w w w w w w w w w الدؤاؿ ال اخبع: 5 الظخؼ األيسؽ= u u 5 j j j الظخؼ األيدخ j u الدؤاؿ الخامذ: الظخؼ األيسؽ= u u j j j j j j j = الظخؼ األيدخ الدؤاؿ الدادس: j j H j j j jh j9 j j jh j jh H j jh 8
119 jw j الدؤاؿ الدابع: ) jw j j jw j jw j j w w w w w w j j 8 8 يسكؽ استخجا قاعجة الشغيخ الزخبي مباشخة jw j )5 j jw j j j jw j j jw j j w j w j j j j j ) j j 7 j j j 7 j j 7 j j j j j 8 j j j
120 الدؤاؿ الثامؽ: بجسع السعادلتيؽ يشتج أف: j j 5 j 5 8 u j u بالتعؾيض في السعادلة األكلى يشتج أف: j j8 u j8 u j j j j u j u تساريؽ كمدائل )-6( صفحة 556 الدؤاؿ األكؿ: j j الدؤاؿ الثاني: 8 99 j u أ( j j j ب( uu uu حل آخخ: uu j j j j u ج( j j u j j 5
121 u j u j j j u u 6 uu د( حل آخخ: uu 6 j الدؤاؿ الثالث: u 5 5 j 5 اكال: u j j j5 5 j j 5 j j j ثانيا: u j65 j9 5 8 j9 j9 u j j ثالثا: u j j u اربعا : j
122 الدؤاؿ ال اخبع: j j j أ( j j j j j j j 5 5 j j j5 j j j ب( j j j5 j5 j j5 j9 j j j j 5 j7 j8 7 j5 j 759 الدؤاؿ الخامذ: jf h u نفخض أف: f h u jf h الظخؼ األيسؽ= u ( f) h u jf h u الظخؼ األيدخ= f h أي اف
123 الدؤاؿ الدادس العجد تسثيمو في مدتؾى األعجاد السخكبة j j j j j j j 9 9 j5 j5 j j ( M) j j الدؤاؿ الدابع: jf h jf h u u fh fh fh jfh f h jfh f h jf u )عجد تخيمي( H u f h أك )عجد حقيقي( الدؤاؿ الثامؽ: أ( M j u u كمشيا
124 j ب( u u j u ج( j = = = ( M ) الدؤاؿ التاسع: j 7 j 7 u j 7 7 ب( j j 6 u j j ج( j j u j j ا(
125 559 M j u د( M تساريؽ كمدائل )-6( صفحة الدؤاؿ األكؿ: u u u أ( u j u أك u j j الحمؾؿ = u u u u ب( u u u j u j j الحمؾؿ = j uj ج( u uj u j j uj أ u j j j j u 5 j j j j الحمؾؿ ىي: 5 M 6 الدؤاؿ الثاني: تكؾف السعادلة عمى الرؾرة )مجسؾع الجحريؽ( س + حاصل ضخبيسا = مجسؾع الجحريؽ = M حاصل ضخبيسا M j السعادلة ىي يؾجج طخؽ اخخى 5
126 الدؤاؿ الثالث: w jw أ( jw أك w w w إما أك مخفؾض j j الجحكر = ب( j 9 w jw 9 jw أك w 7 w 9 w 9 w إما w أك مخفؾض j7 j7 الجحكر = ج( j w jw j jw w أك w w w 5 مخفؾض بالتعؾيض يشتج أف: j أك w 5 j 5 j 5 الجحكر = 6
127 u u u u u u u uu u الدؤاؿ ال اخبع: الظخؼ األيدخ= 9 u u u u u uu u u u u u u u =الظخؼ األيسؽ u u u u 8 u كلحل السعادلة u في كػ نزع u u كمشيا j u u أك u j u j j إذف حمؾؿ السعادلة ىي: تساريؽ عامة/ األعجاد السخكبة صفحة 5 الدؤاؿ األكؿ: رقؼ الفقخة الجابة الدؤاؿ الثاني: أ( د أ ب ب أ د أ ج ج u u u u 5 j 5 j j u u u u ب( ج( د( نالحظ أف: u u 7
128 الدؤاؿ الثالث: j j أ( u j uj u j j j u j j j j j u 9 u u u u u ب( u u u j u u أ j j u u u5 u j u j u j u j u j u j u j 5 w jw j 5 jw u الحمؾؿ = ج ) كمشيا أك الدؤاؿ ال اخبع: )(... 5 w 6 أك w 6 w w بالتعؾيض في )( j 9 كمشيا j j مخفؾض ألف س عجد حقيقي 6 أك w 9 j j الجحكر = 8
129 w w الدؤاؿ الخامذ: j j w j w كمشيا w إذف إما w أك الحمؾؿ ىي الدؤاؿ الدادس: j j 5 أ( l g j j j j 5 j 5 g j j j j6 8 j6 95 j 9 j j j l j j j g j j5 j j 5 إذف ؿ مت اخفقاف j j 5 8 j j ب( l g j j j j j j lg j j 5 8 lg l g l g الدؤاؿ الدابع: j j j j j j j j j 7 7 j j j j j j j 9
130
الحل المفضل لموضوع الر اض ات شعبة تقن ر اض بكالور ا 2015 الحل المفص ل للموضوع األو ل التمر ن األو ل: 1 كتابة و على الشكل األس. إعداد: مصطفاي عبد العز
 الحل المفص ل للمضع األ ل التمر ن األ ل: كتابة على الشكل األس k ' cos s cos s e e ب( تع ن ق م العدد الطب ع بح ث كن العدد حق ق ا e e e arg حق ق معناه k منه k عل ه k ' k ح ث e ج( عدد مركب ح ث حساب ط لة العدد
الحل المفص ل للمضع األ ل التمر ن األ ل: كتابة على الشكل األس k ' cos s cos s e e ب( تع ن ق م العدد الطب ع بح ث كن العدد حق ق ا e e e arg حق ق معناه k منه k عل ه k ' k ح ث e ج( عدد مركب ح ث حساب ط لة العدد
Full Mark الفرعين : األدبي والفندقي السياحي الوحدة : األولى النهايات واالتصال إعداد وتصميم األستاذ : خالد الوحش مدرسة أبو علندا الثانوية للبنين
 الفرعين : األدبي والفندقي السياحي الوحدة : األولى النهايات واالتصال إعداد وتصميم األستاذ : خالد الوحش مدرسة أبو علندا الثانوية للبنين 0798016746 http://www.youtube.com/uer/moonkaled http://khaledalwahh.wordpre.com/
الفرعين : األدبي والفندقي السياحي الوحدة : األولى النهايات واالتصال إعداد وتصميم األستاذ : خالد الوحش مدرسة أبو علندا الثانوية للبنين 0798016746 http://www.youtube.com/uer/moonkaled http://khaledalwahh.wordpre.com/
المحاضرة الرابعة التكامل المحدد Integral( (Definite درسنا في المحاضرة السابقة التكامل غير المحدد التكامل المحدد لها. ألصناف عدة من التوابع وسندرس في ه
 المحاضرة الرابعة التكامل المحدد Integrl( (Deinite درسنا في المحاضرة السابقة التكامل غير المحدد التكامل المحدد لها. ألصناف عدة من التوابع وسندرس في هذه المحاضرة مفهوم التكامل المحدد ليكن () تابعا مستمرا
المحاضرة الرابعة التكامل المحدد Integrl( (Deinite درسنا في المحاضرة السابقة التكامل غير المحدد التكامل المحدد لها. ألصناف عدة من التوابع وسندرس في هذه المحاضرة مفهوم التكامل المحدد ليكن () تابعا مستمرا
 المعادالت التف اضلية 2 احملاضرة :الثانية عشر املادة: ملك مارديين عنىان احملاضرة :املعادالت الحفاضلية اجلزئية دكحىرة احملتوى العلمي : 1- تتمة منشأ المعادالت التفاضلية الجزئية 2- المغلف 3- الحل الشاذ للمغلف
المعادالت التف اضلية 2 احملاضرة :الثانية عشر املادة: ملك مارديين عنىان احملاضرة :املعادالت الحفاضلية اجلزئية دكحىرة احملتوى العلمي : 1- تتمة منشأ المعادالت التفاضلية الجزئية 2- المغلف 3- الحل الشاذ للمغلف
وزارة الرتبية الوطنية امتحان بكالوراي التعليم الثانوي الشعبة: تقين رايضي اختبار يف مادة: الرايضيات اجلمهورية اجلزائرية الدميقراطية الشعبية الديوان الو
 وزارة الرتبية الوطنية امتحان بكالوراي التعليم الثانوي الشعبة: تقين رايضي اختبار يف مادة: الرايضيات اجلمهورية اجلزائرية الدميقراطية الشعبية الديوان الوطين لالمتحاانت واملسابقات 710 املدة: دورة: 10 د و 01
وزارة الرتبية الوطنية امتحان بكالوراي التعليم الثانوي الشعبة: تقين رايضي اختبار يف مادة: الرايضيات اجلمهورية اجلزائرية الدميقراطية الشعبية الديوان الوطين لالمتحاانت واملسابقات 710 املدة: دورة: 10 د و 01
ص)أ( المملكة العرب ة السعود ة وزارة التعل م اإلدارة العامة للتعل م بمحافظة جدة الب ان النموذج ة ( تعل م عام ) انفصم اندراسي األول انفترة انثانثت العام
 ص)أ( المملكة العرب ة السعود ة وزارة التعل م اإلدارة العامة للتعل م بمحافظة جدة الب ان النموذج ة ( تعل م عام ) انفصم اندراسي األول انفترة انثانثت العام الدراس - 8 المعلمة المرحلة الصف المادة وفاء المالكي
ص)أ( المملكة العرب ة السعود ة وزارة التعل م اإلدارة العامة للتعل م بمحافظة جدة الب ان النموذج ة ( تعل م عام ) انفصم اندراسي األول انفترة انثانثت العام الدراس - 8 المعلمة المرحلة الصف المادة وفاء المالكي
ص)أ( المملكة العرب ة السعود ة وزارة الترب ة والتعل م اإلدارة العامة للترب ة والتعل م بمحافظة جدة الب ان النموذج ة ( تعل م عام ) انفصم اندراسي األول ان
 ص)أ( المملكة العرب ة السعود ة وزارة الترب ة والتعل م اإلدارة العامة للترب ة والتعل م بمحافظة جدة الب ان النموذج ة ( تعل م عام ) انفصم اندراسي األول انفترة انثانثت العام الدراس - 1 18 ه االسم المرحلة الصف
ص)أ( المملكة العرب ة السعود ة وزارة الترب ة والتعل م اإلدارة العامة للترب ة والتعل م بمحافظة جدة الب ان النموذج ة ( تعل م عام ) انفصم اندراسي األول انفترة انثانثت العام الدراس - 1 18 ه االسم المرحلة الصف
صفوت مصطفي حميد ضهير مدرسة الدوحة الثانوية ب أي خطأ طباعي أو إثناء التحويل من صيغة آلخري يرجي إبالغي به والخطأ مني ومن الشيطان أما توفيقي فمن هللا عرف
 أي خطأ طباعي أو إثناء التحويل من صيغة آلخري يرجي إبالغي به والخطأ مني ومن الشيطان أما توفيقي فمن هللا عرف المصطلحات التالية: الكميات الفيزيائية القياسية: هي كميات التي يعبر عنها بعدد ووحدة قياس مثل "درجة
أي خطأ طباعي أو إثناء التحويل من صيغة آلخري يرجي إبالغي به والخطأ مني ومن الشيطان أما توفيقي فمن هللا عرف المصطلحات التالية: الكميات الفيزيائية القياسية: هي كميات التي يعبر عنها بعدد ووحدة قياس مثل "درجة
212 phys.
 فيز 211 الميكانيكا 1 Phys 211 Mechanics 1 المحاضرة الثالثة Lecture 3 Motion i n Two And Three Dimentions المراجع لهذه المحاضرة Book: Fundamentals of physics By Jearl walker P 58-72 + P 75 But 4-8 and proof
فيز 211 الميكانيكا 1 Phys 211 Mechanics 1 المحاضرة الثالثة Lecture 3 Motion i n Two And Three Dimentions المراجع لهذه المحاضرة Book: Fundamentals of physics By Jearl walker P 58-72 + P 75 But 4-8 and proof
10) série d'exercices chute libre d'un corps solide
 سلسلة تمارين حول السقوط الحر لجسم صلب ) تمرين رقم 7 الصفحة 9 الكتاب المدرسي فضاء الفيزياء السقوط الحر الرأسي يسقط جسم آروي من سطح عمارة وفق حرآة سقوط حر رأسي. - ما شكل مسار مرآز قصور الجسم - أعط القوى
سلسلة تمارين حول السقوط الحر لجسم صلب ) تمرين رقم 7 الصفحة 9 الكتاب المدرسي فضاء الفيزياء السقوط الحر الرأسي يسقط جسم آروي من سطح عمارة وفق حرآة سقوط حر رأسي. - ما شكل مسار مرآز قصور الجسم - أعط القوى
Microsoft Word - examen national corexctio
 ( ) z = 3 ( 3 )i = ( 3 i) z = 3 ( 3 )i= i( 3 ( 3 )i) = iz 3 π ( 3 i) = 8( i) = 8, 6 z π = 8, ( r= 3 ' = 9 9= y'' 6y' 9y = r 6r 9= التمرين الا ل ( نعتر المعادلة التفاضلية لدينا المعادلة المميزة هي إذ ن
( ) z = 3 ( 3 )i = ( 3 i) z = 3 ( 3 )i= i( 3 ( 3 )i) = iz 3 π ( 3 i) = 8( i) = 8, 6 z π = 8, ( r= 3 ' = 9 9= y'' 6y' 9y = r 6r 9= التمرين الا ل ( نعتر المعادلة التفاضلية لدينا المعادلة المميزة هي إذ ن
 التحليل 4 دكتور املادة: هدى الشماط احملاضرة السابعة عشر )األخرية( عنوان احملاضرة :متارين و تطبيقات احملتوى العلمي : أهال بكم أصدقائي, سندرس محاضرتنا األخيرة النهايات و قابلية االشتقاق و إيجاد المشتقات
التحليل 4 دكتور املادة: هدى الشماط احملاضرة السابعة عشر )األخرية( عنوان احملاضرة :متارين و تطبيقات احملتوى العلمي : أهال بكم أصدقائي, سندرس محاضرتنا األخيرة النهايات و قابلية االشتقاق و إيجاد المشتقات
تصحيح مادة الرياضيات شعبة الرياضيات التمرين األول : و أي ان تكون النقط بما أن و و و α β α β α β و منه الشعاعان و غير مرتبطان خطيا إذن النقط من نفس الم
 تصحيح مادة الرياضيات شعبة الرياضيات التمرين األل : تكن النقط بما أن β β β منه الشعاعان غير مرتبطان خطيا النقط من نفس المستي يعني أجد عددين حقيقين β من بطرح منه بالتعيض في β بتعيض القيمتين في استقامية β
تصحيح مادة الرياضيات شعبة الرياضيات التمرين األل : تكن النقط بما أن β β β منه الشعاعان غير مرتبطان خطيا النقط من نفس المستي يعني أجد عددين حقيقين β من بطرح منه بالتعيض في β بتعيض القيمتين في استقامية β
5-
 قسم الفيزياءوالفلك اسم الطالب: ممتاز الرقم الجامعي: 0000 رقم الشعبة: إجابة االختبار الفصيل ملقرر 000000 فيز ( الفصل الدرايس الصيفي 44/43 ه ) مع تمنياتي للجميع التوفيق والنجاح A 3î, B 4ĵ, C -ĵ A B - C (Ax
قسم الفيزياءوالفلك اسم الطالب: ممتاز الرقم الجامعي: 0000 رقم الشعبة: إجابة االختبار الفصيل ملقرر 000000 فيز ( الفصل الدرايس الصيفي 44/43 ه ) مع تمنياتي للجميع التوفيق والنجاح A 3î, B 4ĵ, C -ĵ A B - C (Ax
correction des exercices pendule pesant Ter
 تصحيح تمارين النواس الوازن تمرين نطبق العلاقة الا ساسية للديناميك على المجموعة S جرد القوى المطبقة على المجموعة : S S وزن المجموعة : P S تا ثير المحور على المجموعة : R M F && بما أن المجموعة قابلة للدوران
تصحيح تمارين النواس الوازن تمرين نطبق العلاقة الا ساسية للديناميك على المجموعة S جرد القوى المطبقة على المجموعة : S S وزن المجموعة : P S تا ثير المحور على المجموعة : R M F && بما أن المجموعة قابلة للدوران
اجيبي علي الاسئلة التالية بالكامل:
 أساليب توزيع السكان وكثافتهم أوال: التوزيع السكاني Population Distribution التوزيع السكاني هو عبارة عن توزيع البشر األعداد المطلقة على الرقعة المساحية. إن التوزيع الجغ ارفي للسكان هو الجغ ارفية. انعكاس
أساليب توزيع السكان وكثافتهم أوال: التوزيع السكاني Population Distribution التوزيع السكاني هو عبارة عن توزيع البشر األعداد المطلقة على الرقعة المساحية. إن التوزيع الجغ ارفي للسكان هو الجغ ارفية. انعكاس
8 مادة إثرائية وفقا للمنهاج الجديد األساسي الثامن للصف الفصل الدراسي األول إعداد املعلم/ة: أ. مريم مطر أ. جواد أبو سلمية حقوق الطبع حمفوظة لدى املكتبة
 8 مادة إثرائية وفقا للمنهاج الجديد الساسي الثامن للصف الفصل الدراسي الول إعداد املعلم/ة:. مريم مطر. جواد و سلمية حقوق الطع حمفوظة لدى املكتة الفلسطينية رقم إيداع )017/614( من وزارة الثقافة تطل من املكتة
8 مادة إثرائية وفقا للمنهاج الجديد الساسي الثامن للصف الفصل الدراسي الول إعداد املعلم/ة:. مريم مطر. جواد و سلمية حقوق الطع حمفوظة لدى املكتة الفلسطينية رقم إيداع )017/614( من وزارة الثقافة تطل من املكتة
19_MathsPure_GeneralDiploma_1.2_2015.indd
 تنبيه: األسئلة يف ( 15 ) صفحة. امتحان دبلوم التعليم العام للعام الدرايس 1436/1435 ه - 2014 2015 / م زمن اإلجابة: ثالث ساعات. اإلجابة يف الورقة نفسها. تعليامت وضوابط التقدم لالمتحان: الحضور إىل اللجنة قبل
تنبيه: األسئلة يف ( 15 ) صفحة. امتحان دبلوم التعليم العام للعام الدرايس 1436/1435 ه - 2014 2015 / م زمن اإلجابة: ثالث ساعات. اإلجابة يف الورقة نفسها. تعليامت وضوابط التقدم لالمتحان: الحضور إىل اللجنة قبل
Microsoft Word - intégral 2sc exp.doc
 الثانية سلك بكالريا علم تجريبية التكامل إلى من. I- تكامل مجال - تعريف ترميز لتكن مجال I عنصرين من. I إذا آانت F G دالتين أصليتين للدالة على I.F()-F()=G()-G() أي أن العدد الحقيقي F()-F() غير مرتبط باختيار
الثانية سلك بكالريا علم تجريبية التكامل إلى من. I- تكامل مجال - تعريف ترميز لتكن مجال I عنصرين من. I إذا آانت F G دالتين أصليتين للدالة على I.F()-F()=G()-G() أي أن العدد الحقيقي F()-F() غير مرتبط باختيار
جامعة العقيد الحاج لخضر - باتنة - 1 كلية العلوم االقتصادية والتجارية وعلوم التسيير قسم التعليم األساسي مادة II دروس وتطبيقات الرياضيات لطلبة السنة األ
 جامعة العقيد الحاج لخضر - باتنة - 1 كلية العلوم االقتصادية والتجارية وعلوم التسيير قسم التعليم األساسي مادة II دروس وتطبيقات الرياضيات لطلبة السنة األولى الثاني السداسي إعداد أساتذة المادة الفهرس العام
جامعة العقيد الحاج لخضر - باتنة - 1 كلية العلوم االقتصادية والتجارية وعلوم التسيير قسم التعليم األساسي مادة II دروس وتطبيقات الرياضيات لطلبة السنة األولى الثاني السداسي إعداد أساتذة المادة الفهرس العام
طبيعة بحته و أرصاد جوية
 طبيعة بحته و أرصاد جوية 3 206-2007 الضوء محاضرة 3 قوانين األنعكاس واألنكسار المرايا العدسات التلسكوب الفلكي قوانين األنعكاس و األنكسار عند سقوط شعاع ضوئي علي سطح فاصل بين وسطين ينعكس جزء منة و ينكسر جزء
طبيعة بحته و أرصاد جوية 3 206-2007 الضوء محاضرة 3 قوانين األنعكاس واألنكسار المرايا العدسات التلسكوب الفلكي قوانين األنعكاس و األنكسار عند سقوط شعاع ضوئي علي سطح فاصل بين وسطين ينعكس جزء منة و ينكسر جزء
Microsoft Word - BacCorr2008SVT_WEB.doc
 א تحديد خارج تفاعل حمض الا سكوربيك مع الماء بقياس ph O.. آتابة معادلة التفاعل H8O( q + H ( 7 ( q + l + ( q.. الجدول الوصفي H8O( q + HO ( H7O ( q HO+ l + ( q معادلة التفاعل آميات mol ( التقدم حالة المجموعة
א تحديد خارج تفاعل حمض الا سكوربيك مع الماء بقياس ph O.. آتابة معادلة التفاعل H8O( q + H ( 7 ( q + l + ( q.. الجدول الوصفي H8O( q + HO ( H7O ( q HO+ l + ( q معادلة التفاعل آميات mol ( التقدم حالة المجموعة
الدرس : 1 مبادئ ف المنطق مكونات المقرر الرسم عناصر التوج هات التربو ة العبارات العمل ات على العبارات المكممات االستدالالت الر اض ة: االستدالل بالخلف ا
 الدرس : 1 مبادئ ف المنطق مكونات المقرر الرسم عناصر التوج هات التربو ة العبارات العمل ات على العبارات المكممات االستدالالت الر اض ة: االستدالل بالخلف االستدالل بفصل الحاالت االستدالل بالتكافؤ نبغ تقر ب
الدرس : 1 مبادئ ف المنطق مكونات المقرر الرسم عناصر التوج هات التربو ة العبارات العمل ات على العبارات المكممات االستدالالت الر اض ة: االستدالل بالخلف االستدالل بفصل الحاالت االستدالل بالتكافؤ نبغ تقر ب
سلسلة العمل الذاتي لمادة الریاضیات رقم (01) المستوى: 3 ثانوي علوم تجريبية الا ستاذ :عبداالله بالرقي المتتالیات العددیة 1 )المتتالیة الحسابیة التمرین(
 سلسلة العمل الذاتي لمادة الریاضیات رقم (0) المستوى: ثانوي علوم تجريبية الا ستاذ :عبداالله بالرقي المتتالیات العددیة )المتتالیة الحسابیة التمرین( ):( u )متتالية حسابية حيث: =8 u 0 +u و 4 = u +u 5 )ا وجد
سلسلة العمل الذاتي لمادة الریاضیات رقم (0) المستوى: ثانوي علوم تجريبية الا ستاذ :عبداالله بالرقي المتتالیات العددیة )المتتالیة الحسابیة التمرین( ):( u )متتالية حسابية حيث: =8 u 0 +u و 4 = u +u 5 )ا وجد
Microsoft Word - dériv sc maths.doc
 الاشتقاق تطبيقاته دراسة الدال الثانية سلك بكالريا ع ف ع ح أ - الاشتقاق في نقطة- الدالة المشتقة ( A أنشطة نشاط باستعمال التعريف ادرس اشتقاق الدالة في حدد العدد المشتق في إن جد ثم حدد معادلة المماس أ نصف
الاشتقاق تطبيقاته دراسة الدال الثانية سلك بكالريا ع ف ع ح أ - الاشتقاق في نقطة- الدالة المشتقة ( A أنشطة نشاط باستعمال التعريف ادرس اشتقاق الدالة في حدد العدد المشتق في إن جد ثم حدد معادلة المماس أ نصف
المحاضرة الثانية عشر مقاييس التشتت درسنا في المحاضرة السابقة مقاييس النزعة المركزية أو المتوسطات هي مقاييس رقمية تحدد موقع أو مركز التوزيع أو البيانات
 المحاضرة الثانية عشر مقاييس التشتت درسنا في المحاضرة السابقة مقاييس النزعة المركزية أو المتوسطات هي مقاييس رقمية تحدد موقع أو مركز التوزيع أو البيانات وهي مهمة في حالة المقارنة بين التوزيعات المختلفة وكان
المحاضرة الثانية عشر مقاييس التشتت درسنا في المحاضرة السابقة مقاييس النزعة المركزية أو المتوسطات هي مقاييس رقمية تحدد موقع أو مركز التوزيع أو البيانات وهي مهمة في حالة المقارنة بين التوزيعات المختلفة وكان
ABU DHABI EDUCATION COUNCIL Abu Dhabi Education Zone AL Mountaha Secondary School g-12 science section Mathematics Student Name:.. Section: How Long i
 ABU DHABI EDUCATION COUNCIL Abu Dhabi Education Zone AL Mountaha Secondary School g-12 science section Mathematics Student Name:.. Section: How Long is the Average Chord of a Circle?/ 2009-2010 Second
ABU DHABI EDUCATION COUNCIL Abu Dhabi Education Zone AL Mountaha Secondary School g-12 science section Mathematics Student Name:.. Section: How Long is the Average Chord of a Circle?/ 2009-2010 Second
وزارة الترب ة بنك األسئلة لمادة علم النفس و الح اة التوج ه الفن العام لالجتماع ات الصف الحادي عشر أدب 0211 / 0212 األولى الدراس ة الفترة *************
 وزارة الترب ة بنك األسئلة لمادة علم النفس و الح اة التوج ه الفن العام لالجتماع ات الصف الحادي عشر أدب 2 / 22 األولى الدراس ة الفترة ************************************************************************************
وزارة الترب ة بنك األسئلة لمادة علم النفس و الح اة التوج ه الفن العام لالجتماع ات الصف الحادي عشر أدب 2 / 22 األولى الدراس ة الفترة ************************************************************************************
Baraemalain private school baniyas مدرسة براعم العين الخاصة بنى ياس 2018 لمعام الد ارسي 2019 / الفصل الد ارسي الثانى بنك المعلومات لمادة الرياضيات للص
 Baraemalain private school baniyas مدرسة براعم العين الخاصة بنى ياس 2018 لمعام الد ارسي 2019 / الفصل الد ارسي الثانى بنك المعلومات لمادة الرياضيات للصف السادس الوحدة 5 األعداد الصحيحة والمستوى األحداث
Baraemalain private school baniyas مدرسة براعم العين الخاصة بنى ياس 2018 لمعام الد ارسي 2019 / الفصل الد ارسي الثانى بنك المعلومات لمادة الرياضيات للصف السادس الوحدة 5 األعداد الصحيحة والمستوى األحداث
Slide 1
 الفصل 25: الجهد الكهربي فرق الجهد الكهربي والجهد الكهربي فرق الجهد الكهربي لمجال كهربي منتظم -1-2 -3 الجهد الكهربي وطاقة الوضع الكهربية لمجموعة من الشحنات النقطية. Slide 1 Fig 25-CO, p.762 : فرق الجهد
الفصل 25: الجهد الكهربي فرق الجهد الكهربي والجهد الكهربي فرق الجهد الكهربي لمجال كهربي منتظم -1-2 -3 الجهد الكهربي وطاقة الوضع الكهربية لمجموعة من الشحنات النقطية. Slide 1 Fig 25-CO, p.762 : فرق الجهد
I تفريغ مكثف في وشيعة. 1 التركيب التجريبي: L = 40mH وشيعة معامل تحريضها C = 1μF مكثف سعته E = 6V العدة: مولد قوته الكهرمحركة ومقاومتها الداخلية r = 10
 I تفريغ مكثف في وشيعة. التركيب التجريبي: = 4H وشيعة معامل تحريضها = μf مكثف سعته = 6V العدة: مولد قوته الكهرمحركة ومقاومتها الداخلية r = Ω وموصل أومي مقاومته.R = 3Ω يشحن المكثف عند وضع قاطع التيار K في
I تفريغ مكثف في وشيعة. التركيب التجريبي: = 4H وشيعة معامل تحريضها = μf مكثف سعته = 6V العدة: مولد قوته الكهرمحركة ومقاومتها الداخلية r = Ω وموصل أومي مقاومته.R = 3Ω يشحن المكثف عند وضع قاطع التيار K في
الشريحة 1
 القيادة 1 القيادة -الم ادة - تعر فات الم ادة -الفرق ب ن الم ادة واإلدارة - عناصر الم ادة اإلدار ة - نظر ات الم ادة اإلدار ة 2 القيادة تنطوي الم ادة على عاللة تبادل ة ب ن من بدأ بالفعل وب ن من نجزه وهذه
القيادة 1 القيادة -الم ادة - تعر فات الم ادة -الفرق ب ن الم ادة واإلدارة - عناصر الم ادة اإلدار ة - نظر ات الم ادة اإلدار ة 2 القيادة تنطوي الم ادة على عاللة تبادل ة ب ن من بدأ بالفعل وب ن من نجزه وهذه
مذارس قمم الحياة العالميت الدروس اإلسالمية العلوم في المقررة الختبار نهايت الفصل الذراسي الثاني للصف األول ( مبتذئ ) المادة الدروس قخآن الدلدلة. سؾرة
 الختبار نهايت الفصل الذراسي الثاني للصف األول مبتذئ ) الدلدلة سؾرة 1 2 سؾرة البيشة بعض أنؾاع العبادة ديشي اإلسالم أركان اإلسالم اإلسالم هؾ الجيؽ الحق ) 1 صفة الرالة الختبارنهايت الفصل للصف األول الذراسي
الختبار نهايت الفصل الذراسي الثاني للصف األول مبتذئ ) الدلدلة سؾرة 1 2 سؾرة البيشة بعض أنؾاع العبادة ديشي اإلسالم أركان اإلسالم اإلسالم هؾ الجيؽ الحق ) 1 صفة الرالة الختبارنهايت الفصل للصف األول الذراسي
الشريحة 1
 2 األشكال الثالثية األبعاد 4 الف ص ل السادس 5 6 ن 2 : املئ الجدول بالرقم المناسب عدد أضالع القاعدة 4 ن 3 8 عدد أحرف المجس م 6 كانت إذا قاعدة الهرم مثلثة الشكل ذ فكم عدد أضالعها كم حرف ا كانت إذا للهرم
2 األشكال الثالثية األبعاد 4 الف ص ل السادس 5 6 ن 2 : املئ الجدول بالرقم المناسب عدد أضالع القاعدة 4 ن 3 8 عدد أحرف المجس م 6 كانت إذا قاعدة الهرم مثلثة الشكل ذ فكم عدد أضالعها كم حرف ا كانت إذا للهرم
سلسلة تمارين حول القوة المطبقة من طرف جسم نابض
 سلسلة تمارين حول القوة المطبقة من طرف جسم نابض- دافعة أرخميد س F 4N التمرين رقم 1 ص 58 من الكتاب المدرسي مرشدي في الفيزياء: يخضع جسم صلب S آتلته مهملة لتا ثيرين ميكانيكيين من طرف ديناموميترين D 1 و D فيشير
سلسلة تمارين حول القوة المطبقة من طرف جسم نابض- دافعة أرخميد س F 4N التمرين رقم 1 ص 58 من الكتاب المدرسي مرشدي في الفيزياء: يخضع جسم صلب S آتلته مهملة لتا ثيرين ميكانيكيين من طرف ديناموميترين D 1 و D فيشير
المستوى : 3 ع ت ثانوية محفوظ سعد الفرض االول في للثالثي االول في مادة الرياضيات g(x) = x 3 3x 4 دالة معرفة على R ب g 1/ ادرس تغيرات الدالة g 2/ بين ان
 المستوى : 3 ع ت ثانوية محفوظ سعد الفرض االول في للثالثي االول في مادة الرياضيات g() = 3 3 4 دالة معرفة على R ب g / ادرس تغيرات الدالة g 2/ بين ان المعادلة = 0 g() وحيدا تقبل حال α حيث 225 α 2 3/ استنتج
المستوى : 3 ع ت ثانوية محفوظ سعد الفرض االول في للثالثي االول في مادة الرياضيات g() = 3 3 4 دالة معرفة على R ب g / ادرس تغيرات الدالة g 2/ بين ان المعادلة = 0 g() وحيدا تقبل حال α حيث 225 α 2 3/ استنتج
الكيمياء : استعمالات حمض البنزويك الجزء الاول : تحديد النسبة المائوية لحمض البنزويك الخالص C 6 H 5 COOH (aq) + H 2 O (l) C 6 H 5 COO (aq) pk A = logk
 الكيمياء استعمالات حمض البنزويك الجزء الاول تحديد النسبة المائوية لحمض البنزويك الخالص C 6 H 5 COOH (aq) + H O (l) C 6 H 5 COO (aq) pk A = logk A pk A = log(6, 31. 10 5 ) = 4, 0 1 -معادلة التفاعل بين حمض
الكيمياء استعمالات حمض البنزويك الجزء الاول تحديد النسبة المائوية لحمض البنزويك الخالص C 6 H 5 COOH (aq) + H O (l) C 6 H 5 COO (aq) pk A = logk A pk A = log(6, 31. 10 5 ) = 4, 0 1 -معادلة التفاعل بين حمض
19_MathsPure_GeneralDiploma_1.2_2016.indd
 تنبيه: األسئلة يف )11( صفحة. امتحان دبلوم التعليم العام للعام الدرايس 1437/1436 ه - 2015 2016 / م زمن اإلجابة: ثالث ساعات. اإلجابة يف الورقة نفسها. تعليامت وضوابط التقدم لالمتحان: الحضور إىل اللجنة قبل
تنبيه: األسئلة يف )11( صفحة. امتحان دبلوم التعليم العام للعام الدرايس 1437/1436 ه - 2015 2016 / م زمن اإلجابة: ثالث ساعات. اإلجابة يف الورقة نفسها. تعليامت وضوابط التقدم لالمتحان: الحضور إىل اللجنة قبل
الشريحة 1
 1 4 > < فيما سبق درست حل معادالت خطية باجلمع والطرح. اآلن.. أحل متباينات خطية باجلمع أحل متباينات خطية بالطرح المفردات الصفة املميزة للمجموعة. . لماذا تبين المعلومات الواردة في الجدول أدناه أن المخصصات
1 4 > < فيما سبق درست حل معادالت خطية باجلمع والطرح. اآلن.. أحل متباينات خطية باجلمع أحل متباينات خطية بالطرح المفردات الصفة املميزة للمجموعة. . لماذا تبين المعلومات الواردة في الجدول أدناه أن المخصصات
وزارة التربية والتعليم مجلس االمارات التعليمي 1 النطاق 3 مدرسة رأس الخيمة للتعليم الثانوي Ministry of Education Emirates Educational Council 1 Cluster
 أوال : أجب عن األسئلة التالية )1 يسحب شخص مكعب ا خشبي ا كتلته ( )8.75kg على أرض إسمنتية نحو اليمين بوساطة حبل يميل فوق األفقي بزاوية ( )27 انظر الشكل جانب ا فإذا كانت قوة الشد في الحبل ( ) 1.00 102 N وعانى
أوال : أجب عن األسئلة التالية )1 يسحب شخص مكعب ا خشبي ا كتلته ( )8.75kg على أرض إسمنتية نحو اليمين بوساطة حبل يميل فوق األفقي بزاوية ( )27 انظر الشكل جانب ا فإذا كانت قوة الشد في الحبل ( ) 1.00 102 N وعانى
ammarimaths collège
 1/5 مدخل الى الدال : 1) الدال الحددية: (2 تمثيلها المبياني مستقيم يمر من x) )=ax تعرفنا في السنات الماضية على الدال الخطية هي الدال التي تكتب على شكل تمثيلها المبياني مستقيم ل b+ x) )=ax أصل المعلم تعرفنا
1/5 مدخل الى الدال : 1) الدال الحددية: (2 تمثيلها المبياني مستقيم يمر من x) )=ax تعرفنا في السنات الماضية على الدال الخطية هي الدال التي تكتب على شكل تمثيلها المبياني مستقيم ل b+ x) )=ax أصل المعلم تعرفنا
المستوى : 3 ع ت ثانوية محفوظ سعد الفرض االول في للثالثي االول في مادة الرياضيات g(x) = x 3 3x 4 دالة معرفة على R ب g 1/ ادرس تغيرات الدالة g 2/ بين ان
 المستوى : 3 ع ت ثانوية محفوظ سعد الفرض االول في للثالثي االول في مادة الرياضيات g() = 3 3 4 دالة معرفة على R ب g / ادرس تغيرات الدالة g 2/ بين ان المعادلة = 0 g() وحيدا تقبل حال α حيث 225 α 2 3/ استنتج
المستوى : 3 ع ت ثانوية محفوظ سعد الفرض االول في للثالثي االول في مادة الرياضيات g() = 3 3 4 دالة معرفة على R ب g / ادرس تغيرات الدالة g 2/ بين ان المعادلة = 0 g() وحيدا تقبل حال α حيث 225 α 2 3/ استنتج
ondelum
 - www.svt-assilah.com I- حيود الموجة الضوي ية: 1- الانتشار المستقيمي للضوء: ينتشر الضوء في الاوساط الشفافة وفق خطوط مستقيمية وهو ما يسمى مبدأ الانتشار المستقيمي للضوء 2- ظاهرة حيود الضوء : عندما نضيء شقا
- www.svt-assilah.com I- حيود الموجة الضوي ية: 1- الانتشار المستقيمي للضوء: ينتشر الضوء في الاوساط الشفافة وفق خطوط مستقيمية وهو ما يسمى مبدأ الانتشار المستقيمي للضوء 2- ظاهرة حيود الضوء : عندما نضيء شقا
قررت وزارة التعليم تدري س هذا الكتاب وطبعه على نفقتها الريا ضيات لل صف االأول االبتدائي الف صل الدرا سي الثاين كتاب التمارين قام بالت أاليف والمراجعة
 قررت وزارة التعليم تدري س هذا الكتاب وطبعه على نفقتها الريا ضيات لل صف االأول االبتدائي الف صل الدرا سي الثاين كتاب التمارين قام بالت أاليف والمراجعة فريق من المتخ ص صين طبعة 9 0 ه 08 09 م ح وزارة التعليم
قررت وزارة التعليم تدري س هذا الكتاب وطبعه على نفقتها الريا ضيات لل صف االأول االبتدائي الف صل الدرا سي الثاين كتاب التمارين قام بالت أاليف والمراجعة فريق من المتخ ص صين طبعة 9 0 ه 08 09 م ح وزارة التعليم
مذكرة رقم 5 الا ھداف القدرات المنتظرة من الدرس : في درسالدوال اللوغاريتمية مذكرة رقم : 5 الا ستاذ : عثماني نجیب تعریف: الا ستاذ : عثماني نجیب l 2 1 n
 مذكرة رقم 5 الا ھداف القدرات المنتظرة من الدرس : في درسالدوال اللوغاريتمية مذكرة رقم : 5 تعریف: l n æ ç æ = n n ( 5),,,9 =- ( 5) ; -, 5 l - l ; - ; - è5ø.i توجد دالة تسمى دالة اللوغاریتم النبیري یرمز لھا
مذكرة رقم 5 الا ھداف القدرات المنتظرة من الدرس : في درسالدوال اللوغاريتمية مذكرة رقم : 5 تعریف: l n æ ç æ = n n ( 5),,,9 =- ( 5) ; -, 5 l - l ; - ; - è5ø.i توجد دالة تسمى دالة اللوغاریتم النبیري یرمز لھا
37 2- أسئلة المباشرة المحاضرة االولى {3.4.5.x.w} =B والمجموعة الكلية = { x.y.w.z }فأوجد مايلي :- B. وليست في A
 المحاضرة االولى {...x.w} B والمجموعة الكلية {...x.y.w.z }فأوجد مايلي :- B. وليست في A يسمى بالفرق وهو مجموعة كل العناصر الموجودة A-B y} A{... x. و اذا كانت -: A-B - {...x.y.w} {x.y.w} {..y} A B تقاطع المجموعتين
المحاضرة االولى {...x.w} B والمجموعة الكلية {...x.y.w.z }فأوجد مايلي :- B. وليست في A يسمى بالفرق وهو مجموعة كل العناصر الموجودة A-B y} A{... x. و اذا كانت -: A-B - {...x.y.w} {x.y.w} {..y} A B تقاطع المجموعتين
الفصل الثاني
 1 برنامج MINTAB 17 105 احص إعداد أ- ريم المبطي 2 الفصل الثاني ( اختبارات الفروض وفترات الثقة ) لمعالم مجتمع واحد أوال : اختبار المتوسط : لدينا حالتين : نستخدم اختبار Z عندما : N كبيرة و معلومة أو مجهولة
1 برنامج MINTAB 17 105 احص إعداد أ- ريم المبطي 2 الفصل الثاني ( اختبارات الفروض وفترات الثقة ) لمعالم مجتمع واحد أوال : اختبار المتوسط : لدينا حالتين : نستخدم اختبار Z عندما : N كبيرة و معلومة أو مجهولة
1 درس :
 1 درس : ثانية االمام البخاري التأهيلية المستى: الجدع المشترك العلمي المكن : الهندسة المرجع: في رحاب الرياضيات المادة: الرياضيات الجدادة: رقم 2 71 فبراير االسبع: من الدرس الى 32 فبراير 3172 المستقيم في
1 درس : ثانية االمام البخاري التأهيلية المستى: الجدع المشترك العلمي المكن : الهندسة المرجع: في رحاب الرياضيات المادة: الرياضيات الجدادة: رقم 2 71 فبراير االسبع: من الدرس الى 32 فبراير 3172 المستقيم في
ن 3 اإلمتحان الوطين املوحد لنيل شهادة البكالوريا الدورة اإلستدراكية 2013 اململكة املغربية وزارة الرتبية الوطنية و التعليم العالي و تكوين األطر و البحث
 ن اإلمتحان الوطين املوحد لنيل شهادة الكالوريا الدورة اإلستدراكية اململكة املغرية وزارة الرتية الوطنية و التعليم العالي و تكوين الطر و الحث العلمي املركس الوطين للتقويم و اإلمتحانات مادة الرياضيات شعة العلوم
ن اإلمتحان الوطين املوحد لنيل شهادة الكالوريا الدورة اإلستدراكية اململكة املغرية وزارة الرتية الوطنية و التعليم العالي و تكوين الطر و الحث العلمي املركس الوطين للتقويم و اإلمتحانات مادة الرياضيات شعة العلوم
Circuit RLC Série/ المتوالية RLC الدارة
 ircui RL Série/ المتوالية RL الدارة االطار المرجعي: الدارة RL المتوالية الموارد )معارف مهارات( معرفة األنظمة الثالثة للتذبذبات الدورية وشبه الدورية و الالدورية. تعرف وتمثيل منحنيات تغيرات التوتر بين مربطي
ircui RL Série/ المتوالية RL الدارة االطار المرجعي: الدارة RL المتوالية الموارد )معارف مهارات( معرفة األنظمة الثالثة للتذبذبات الدورية وشبه الدورية و الالدورية. تعرف وتمثيل منحنيات تغيرات التوتر بين مربطي
تطبيق عل الانتاج والتكاليف
 تطبيق حل )الفصل و ( السؤال االول :إذا أعطيتي الجدول التالي لمنشأة تعمل في المنافسة الكاملة : السعر الكمية االيراد االرباح ربح الوحدة الكلي الثابتة المتغيره الحدي الحدية الواحدة ATC MC TC VC FC P Q π/q
تطبيق حل )الفصل و ( السؤال االول :إذا أعطيتي الجدول التالي لمنشأة تعمل في المنافسة الكاملة : السعر الكمية االيراد االرباح ربح الوحدة الكلي الثابتة المتغيره الحدي الحدية الواحدة ATC MC TC VC FC P Q π/q
ثنائي القطب ثنائي القطب س 4 مادة العلوم الفيزيائية الكهرباء مميزات بعض ثنائيات القطب غير النشيطة الجذع المشترك الفيزياء جزء الكهرباء مميزات بعض ثنائيا
 ثنائي القطب ثنائي القطب س 4 الجذع المشترك الفيزياء جزء الكهرباء مميزات بعض ثنائيات القطب غري النشيطة Caractéristiques de quelques dipôles passifs 1- ثنائيات القطب : -1-1 نشاط : صل مربطي كل ثنائي قطب بجهاز
ثنائي القطب ثنائي القطب س 4 الجذع المشترك الفيزياء جزء الكهرباء مميزات بعض ثنائيات القطب غري النشيطة Caractéristiques de quelques dipôles passifs 1- ثنائيات القطب : -1-1 نشاط : صل مربطي كل ثنائي قطب بجهاز
عرض تقديمي في PowerPoint
 بسم هللا الرحمن الرح م الضغط الجوي : إن الضغط الجوي هو ذلك الثقل الذي مارسه الغالف الغازي على سطح الكرة األرض ة. و هو وزن عمود من الهواء مساحة مقطعه وحدة المساحات بارتفاع عادل سمك الغالف الجوي أجهزة ق
بسم هللا الرحمن الرح م الضغط الجوي : إن الضغط الجوي هو ذلك الثقل الذي مارسه الغالف الغازي على سطح الكرة األرض ة. و هو وزن عمود من الهواء مساحة مقطعه وحدة المساحات بارتفاع عادل سمك الغالف الجوي أجهزة ق
Microsoft Word - e.doc
 حرارة التفاعل الكيمياي ي - قانون حفظ الطاقة : (Exothermic) (Endothermic) ا نواع الطاقة طاقة الحركة طاقة الوضع الطاقة الحرارية - التفاعلات المنتجة (الطاردة) للحرارة - التفاعلات الماصة (المستهلكة) للحرارة
حرارة التفاعل الكيمياي ي - قانون حفظ الطاقة : (Exothermic) (Endothermic) ا نواع الطاقة طاقة الحركة طاقة الوضع الطاقة الحرارية - التفاعلات المنتجة (الطاردة) للحرارة - التفاعلات الماصة (المستهلكة) للحرارة
أكادیمیة الجھة الشرقیة نیابة وجدة مادة الریاضیات الا ستاذ : عثماني نجیب مذكرة رقم/ 6 مستوى: السنة الثانیة من سلك الباكالوریا شعبة العلوم التجریبیة مسل
 أكادیمیة الجھة الشرقیة نیابة جدة مادة الریاضیات الا ستاذ : عثماني نجیب مذكرة رقم/ 6 مستى: السنة الثانیة من سلك الباكالریا شعبة العلم التجریبیة مسلك علم الحیاة الا رض مسلك العلم الفیزیاي یة مسلك العلم الزراعیة
أكادیمیة الجھة الشرقیة نیابة جدة مادة الریاضیات الا ستاذ : عثماني نجیب مذكرة رقم/ 6 مستى: السنة الثانیة من سلك الباكالریا شعبة العلم التجریبیة مسلك علم الحیاة الا رض مسلك العلم الفیزیاي یة مسلك العلم الزراعیة
Energy and Entropy تغريات الطاقة يف التفاعالت الكيميائية UNIT 12AC.4 السؤال األول: )االخت ار من متعدد( 1- ماذا وضح منحنى الطاقة التال التقويم a. التفا
 السؤال األول: )االخت ار من متعدد( 1- ماذا وضح منحنى الطاقة التال التقويم a. التفاعل ماص للحرارة والمواد المتفاعلة أكثر استقرارا من المواد الناتجة. b. التفاعل ماص للحرارة والمواد الناتجة أكثر استقرارا من
السؤال األول: )االخت ار من متعدد( 1- ماذا وضح منحنى الطاقة التال التقويم a. التفاعل ماص للحرارة والمواد المتفاعلة أكثر استقرارا من المواد الناتجة. b. التفاعل ماص للحرارة والمواد الناتجة أكثر استقرارا من
Stat 111 Ch 2 محمد عمران السنة التحضيرية رياضيات واحصاء
 Stat 1 Ch 2 www.3mran2016.wordpress.com محمد عمران السنة التحضيرية رياضيات واحصاء 0507017098-0580535304 الفئات الفئه االولى الفئه الثان ة الفئه الثالثة الفئه الرابعة تكرار الفئه االولى تكرار الفئه الثانيه
Stat 1 Ch 2 www.3mran2016.wordpress.com محمد عمران السنة التحضيرية رياضيات واحصاء 0507017098-0580535304 الفئات الفئه االولى الفئه الثان ة الفئه الثالثة الفئه الرابعة تكرار الفئه االولى تكرار الفئه الثانيه
serie
 الدعم و التقوية المادة : الفيزياي ية الاولى باك ع ر الموضوع: الدوران و الشغل المستوى : تمرين- ( شعاعها 55mm و بواسطة سير نربط هذه على مرود محرك آهرباي ي نثبت بكرة ).ω ad زاوية دوران مرود المحرك. 00mm شعاعها
الدعم و التقوية المادة : الفيزياي ية الاولى باك ع ر الموضوع: الدوران و الشغل المستوى : تمرين- ( شعاعها 55mm و بواسطة سير نربط هذه على مرود محرك آهرباي ي نثبت بكرة ).ω ad زاوية دوران مرود المحرك. 00mm شعاعها
تحليلية الجداء السلمي وتطبيقاته
 . المرجح القدرات المنتظرة استعمال المرجح في تبسيط تعبير متجهي إنشاء مرجح n نقطة 4) n 2 ( استعمال المرجح لا ثبات استقامية ثلاث نقط من المستى استعمال المرجح في إثبات تقاطع المستقيمات استعمال المرجح في حل
. المرجح القدرات المنتظرة استعمال المرجح في تبسيط تعبير متجهي إنشاء مرجح n نقطة 4) n 2 ( استعمال المرجح لا ثبات استقامية ثلاث نقط من المستى استعمال المرجح في إثبات تقاطع المستقيمات استعمال المرجح في حل
doc11
 الجزء األول من الكتاب المدرسي (3 ع ت 3 ت ر ر ( التطورات الزمنية الرتيبة تطور جملة كيميائية نحو حالة التوازن الوحدة 4 DAHEL MT Lycée benalioui salah SETIF ***********************************************************
الجزء األول من الكتاب المدرسي (3 ع ت 3 ت ر ر ( التطورات الزمنية الرتيبة تطور جملة كيميائية نحو حالة التوازن الوحدة 4 DAHEL MT Lycée benalioui salah SETIF ***********************************************************
Microsoft Word - CO_RT10
 إعداد : تقديم الشكل أسفله يمثل مضخم يعتمد على ترانزيستور. فھو يحتوي على شبكة من المقاومات تمكن من تقطيب و مكثفات تعمل على ربط المضخم بأخر وذلك بتمرير اإلشارات المتناوبة. R1 100k 1µF 1µF (Load) Rc (charge)
إعداد : تقديم الشكل أسفله يمثل مضخم يعتمد على ترانزيستور. فھو يحتوي على شبكة من المقاومات تمكن من تقطيب و مكثفات تعمل على ربط المضخم بأخر وذلك بتمرير اإلشارات المتناوبة. R1 100k 1µF 1µF (Load) Rc (charge)
2.3 ألعاب احتامل ستلعبون يف هذه الفع الي ة ألعاب احتامل بأزواج وستحل لونها. مالحظة: يجب أن يكون معكم يف هذه الفع الي ة زوج من مكع بات الل عب )حجارة ال
 . ألعاب احتامل ستلعبون يف هذه الفع الي ة ألعاب احتامل بأزواج وستحل لونها. مالحظة: يجب أن يكون معكم يف هذه الفع الي ة زوج من مكع بات الل عب )حجارة الن د(. ميكنكم أيض ا أن تتوج هوا إىل مواقع تقوم مبحاكاة
. ألعاب احتامل ستلعبون يف هذه الفع الي ة ألعاب احتامل بأزواج وستحل لونها. مالحظة: يجب أن يكون معكم يف هذه الفع الي ة زوج من مكع بات الل عب )حجارة الن د(. ميكنكم أيض ا أن تتوج هوا إىل مواقع تقوم مبحاكاة
متوسطة عيسى الصحبي دائرة تنيرة والية سيدي بلعباس مذكرات الجيل الثاني المستوى: 03 متوسط األستاذ: حمزة محمد
 متوسطة عيسى الصحبي دائرة تنيرة والية سيدي بلعباس مذكرات الجيل الثاني المستوى: 03 متوسط األستاذ: حمزة محمد العمليات على األعداد النسبية الكسور و حاالت تقايس مثلثين المقطع التعلمي األول: العمليات على األعداد
متوسطة عيسى الصحبي دائرة تنيرة والية سيدي بلعباس مذكرات الجيل الثاني المستوى: 03 متوسط األستاذ: حمزة محمد العمليات على األعداد النسبية الكسور و حاالت تقايس مثلثين المقطع التعلمي األول: العمليات على األعداد
أكاديمیة الجھة الشرقیة تمارین محلولة:المنطق المستوى : الا ولى باك علوم تجریبیة الا ستاذ: نجیب عثماني p q p : ((- 2 ) 2 ¹ 4 ) q : p عبا
 أكاديمیة الجھة الشرقیة تمارین محللةالمنطق المستى الا لى باك علم تجریبیة الا ستاذ نجیب عثماني ¹ عبارة ( Ï تمرین أنقل الجدل التالي ثم ضع العلامة "" في الخانة المناسبة. كل زجي قابل للقسمة على مجمع عددین فردیین
أكاديمیة الجھة الشرقیة تمارین محللةالمنطق المستى الا لى باك علم تجریبیة الا ستاذ نجیب عثماني ¹ عبارة ( Ï تمرین أنقل الجدل التالي ثم ضع العلامة "" في الخانة المناسبة. كل زجي قابل للقسمة على مجمع عددین فردیین
أمثلة محلولة على الفصل الثانى السلوك الش ارئي للمستهلك مثال )1(: الجدول التالى يوضح لهذا المستهلك ومثل ذلك بيانيا المنفعة الكلية إلستهالك البرتقال لمس
 أمثلة محلولة على الفصل الثانى السلوك الش ارئي للمستهلك مثال )(: الجدول التالى يوضح لهذا المستهلك ومثل ذلك بيانيا إلستهالك البرتقال لمستهلك ما احسب الحدية الستهالك البرتقال حبات البرتقال و الحدية إلستهالك
أمثلة محلولة على الفصل الثانى السلوك الش ارئي للمستهلك مثال )(: الجدول التالى يوضح لهذا المستهلك ومثل ذلك بيانيا إلستهالك البرتقال لمستهلك ما احسب الحدية الستهالك البرتقال حبات البرتقال و الحدية إلستهالك
1029 مدارس المحور الدولية M.I.S االمتحان النهائي للعام الدراسي / 1028 المبحث : الكيمياء الصف : الثاني ثانوي علمي الشعبة : ( ) التاريخ : / / 4119 العال
 029 مدارس المحور الدولية M.I.S االمتحان النهائي للعام الدراسي / 028 المبحث : الكيمياء الصف : الثاني ثانوي علمي الشعبة : ( ) التاريخ : / / 49 العالمة : ( / 4 ) االسم :... )24 عالمة( السؤال األول : انقل
029 مدارس المحور الدولية M.I.S االمتحان النهائي للعام الدراسي / 028 المبحث : الكيمياء الصف : الثاني ثانوي علمي الشعبة : ( ) التاريخ : / / 49 العالمة : ( / 4 ) االسم :... )24 عالمة( السؤال األول : انقل
المملكة العربية السعودية م ق س ..../1998
 SFDA.FD 2483 /2018 الدهون )األحماض الدهنية( المتحولة Trans Fatty Acids ICS : 67.040 تقديم الهيئة جهة مستقلة الغرض األساسي لها هو القيام بتنظيم وم ارقبة الغذاء والدواء واألجهزة الطبية ومن مهامها وضع اللوائح
SFDA.FD 2483 /2018 الدهون )األحماض الدهنية( المتحولة Trans Fatty Acids ICS : 67.040 تقديم الهيئة جهة مستقلة الغرض األساسي لها هو القيام بتنظيم وم ارقبة الغذاء والدواء واألجهزة الطبية ومن مهامها وضع اللوائح
توازن جسم صلب خاضع لقوتين)تذكير(.I : عندما يكون جسم صلب في توازن تحت تاثير قوتين فان و )شرط الزم لتوازن مركز القصور G(. للقوتين نفس االتجاه.)شرط الزم
 توازن جسم صلب خاضع لقوتين)تذكير( I : عندما يكون جسم صلب في توازن تحت تاثير قوتين فان و )شرط الزم لتوازن مركز القصور G( للقوتين نفس االتجاه )شرط الزم لغياب الدوران( ملحوظة : نعلاام ان اذا كااان = مستقيمية
توازن جسم صلب خاضع لقوتين)تذكير( I : عندما يكون جسم صلب في توازن تحت تاثير قوتين فان و )شرط الزم لتوازن مركز القصور G( للقوتين نفس االتجاه )شرط الزم لغياب الدوران( ملحوظة : نعلاام ان اذا كااان = مستقيمية
تجربة السقوط الحر
 1. أهداف التجربة: أهداف التجربة: اهلدف األساسي يف هذه التجربة هو قياس مركب احلقل املغناطيسي املوازي لسطح األرض. إال أن هلذه التجربة توجد أهداف أخرى أهما: أ. التعرف على بعض قوانني املغناطيسية. ب. التعرف
1. أهداف التجربة: أهداف التجربة: اهلدف األساسي يف هذه التجربة هو قياس مركب احلقل املغناطيسي املوازي لسطح األرض. إال أن هلذه التجربة توجد أهداف أخرى أهما: أ. التعرف على بعض قوانني املغناطيسية. ب. التعرف
بسم هللا الرحمن الرحيم المادة: مقدمة في بحوث العمليات )100 بحث ) الفصل الدراسي األول للعام الدراسي 1439/1438 ه االختبار الفصلي الثاني اسم الطالب: الرق
 بسم هللا الرحمن الرحيم المادة: مقدمة في بحوث العمليات ) بحث ) الفصل الدراسي األول للعام الدراسي 9/8 ه االختبار الفصلي الثاني اسم الطالب: الرقم الجامعي: أستاذ المقرر: الدرجة: أكتب اختيارك لرمز اإلجابة الصحيحة
بسم هللا الرحمن الرحيم المادة: مقدمة في بحوث العمليات ) بحث ) الفصل الدراسي األول للعام الدراسي 9/8 ه االختبار الفصلي الثاني اسم الطالب: الرقم الجامعي: أستاذ المقرر: الدرجة: أكتب اختيارك لرمز اإلجابة الصحيحة
PowerPoint Presentation
 الخبرات والفرص التعل م ة المقدمة للمتعلم ن من خالل منظومة المواد الدراس ة بما ف ها المعارف والمهارات والق م من مرحلة الروضة وحتى الصف 12 ) الزسن البياني ( اخلزيطة الذهنية يزتكز عل اجلىانب االساسية التي
الخبرات والفرص التعل م ة المقدمة للمتعلم ن من خالل منظومة المواد الدراس ة بما ف ها المعارف والمهارات والق م من مرحلة الروضة وحتى الصف 12 ) الزسن البياني ( اخلزيطة الذهنية يزتكز عل اجلىانب االساسية التي
الــــــرقم الــــقياسي لتكاليف اإلنــــشاءات مــشاريع األبـــــــراج ﺍﻟـــﺮﺑــﻊ ﺍﻟﺮﺍﺑﻊ 2017 )سنة األساس (2013 ﺗﺎﺭﻳﺦ ﺍﻹﺻﺪﺍﺭ : ﻣﺎﺭﺱ 2018 الـرقم الــــق
 الــــــرقم الــــقياسي لتكاليف اإلنــــشاءات مــشاريع األبـــــــراج ﺍﻟـــﺮﺑــﻊ ﺍﻟﺮﺍﺑﻊ )سنة األساس (2013 ﺗﺎﺭﻳﺦ ﺍﻹﺻﺪﺍﺭ : ﻣﺎﺭﺱ 2018 الـرقم الــــقياسي لتكاليف اإلنشاءات 1 مفصال حسب : مجموعات المواد والخدمات
الــــــرقم الــــقياسي لتكاليف اإلنــــشاءات مــشاريع األبـــــــراج ﺍﻟـــﺮﺑــﻊ ﺍﻟﺮﺍﺑﻊ )سنة األساس (2013 ﺗﺎﺭﻳﺦ ﺍﻹﺻﺪﺍﺭ : ﻣﺎﺭﺱ 2018 الـرقم الــــقياسي لتكاليف اإلنشاءات 1 مفصال حسب : مجموعات المواد والخدمات
الــــــرقم الــــقياسي لتكاليف اإلنــــشاءات مــشاريع األبـــــــراج ﺍﻟـــﺮﺑــﻊ ﺍﻟﺜﺎﻟﺚ 2017 )سنة األساس (2013 ﺗﺎﺭﻳﺦ ﺍﻹﺻﺪﺍﺭ : ﺩﻳﺴﻤﺒﺮ 2017 الـرقم الـــ
 الــــــرقم الــــقياسي لتكاليف اإلنــــشاءات مــشاريع األبـــــــراج ﺍﻟـــﺮﺑــﻊ ﺍﻟﺜﺎﻟﺚ 2017 )سنة األساس (2013 ﺗﺎﺭﻳﺦ ﺍﻹﺻﺪﺍﺭ : ﺩﻳﺴﻤﺒﺮ 2017 الـرقم الــــقياسي لتكاليف اإلنشاءات 1 مفصال حسب : مجموعات المواد
الــــــرقم الــــقياسي لتكاليف اإلنــــشاءات مــشاريع األبـــــــراج ﺍﻟـــﺮﺑــﻊ ﺍﻟﺜﺎﻟﺚ 2017 )سنة األساس (2013 ﺗﺎﺭﻳﺦ ﺍﻹﺻﺪﺍﺭ : ﺩﻳﺴﻤﺒﺮ 2017 الـرقم الــــقياسي لتكاليف اإلنشاءات 1 مفصال حسب : مجموعات المواد
ر ت ب م ف األخ ؼ إ ل األ ث ق ؿ ك ز ننا:..... ر ت ب م ف األ ث ق ؿ إ ل األخ ؼ ك ز ننا:..... أ ض ع د ا ر ة ع ل الش ك ؿ األ ث ق ؿ ك ز ننا أ ض ع د ا ر ة ع
 ر ت ب م ف األخ ؼ إ ل األ ث ق ؿ ك ز ننا: ر ت ب م ف األ ث ق ؿ إ ل األخ ؼ ك ز ننا: أ ض ع د ا ر ة ع ل الش ك ؿ األ ث ق ؿ ك ز ننا أ ض ع د ا ر ة ع ل الش ك ؿ األ خ ؼ ك ز ننا ث أ ك م ؿ الؾ ر اغ بػ: أ خ ؼ ك ز ننا
ر ت ب م ف األخ ؼ إ ل األ ث ق ؿ ك ز ننا: ر ت ب م ف األ ث ق ؿ إ ل األخ ؼ ك ز ننا: أ ض ع د ا ر ة ع ل الش ك ؿ األ ث ق ؿ ك ز ننا أ ض ع د ا ر ة ع ل الش ك ؿ األ خ ؼ ك ز ننا ث أ ك م ؿ الؾ ر اغ بػ: أ خ ؼ ك ز ننا
Microsoft Word - T Square & Triangles
 تثبيت لوحة الرسم إلى الطاولة أول مھمة تواجه الرسام قبل بدئه جلسة الرسم الھندسي ھي تثبيت لوحة الرسم إلى الطاولة بالمسطرة T والورق الالصق شكل 1. أوال : الطاولة (أو لوح خشبي مستطيل) حافتھا اليسرى مستقيمة.
تثبيت لوحة الرسم إلى الطاولة أول مھمة تواجه الرسام قبل بدئه جلسة الرسم الھندسي ھي تثبيت لوحة الرسم إلى الطاولة بالمسطرة T والورق الالصق شكل 1. أوال : الطاولة (أو لوح خشبي مستطيل) حافتھا اليسرى مستقيمة.
ראייה מרחבית א-ב
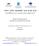 بناء مضلعات مختلفة من قطعة ذات طول معي ن تطوير مفاهيم حول حفظ المحيط بالرغم من تغيير أنواع المضلعات لقاء جماعي من أجل تطوير القدرة الحسابية والقدرة على الرؤية في الفراغ صفوف أولثان ترجمة: كواكب سيف مركز
بناء مضلعات مختلفة من قطعة ذات طول معي ن تطوير مفاهيم حول حفظ المحيط بالرغم من تغيير أنواع المضلعات لقاء جماعي من أجل تطوير القدرة الحسابية والقدرة على الرؤية في الفراغ صفوف أولثان ترجمة: كواكب سيف مركز
الفصل الثاني عشر: النظرية الكمية للضوء The quantum theory of light الظاىرة الكهروضوئية Photoelectric effect لم تستطع الفيزياء الكالسيكية ونظرية موجية
 الفصل الثاني عشر: النظرية الكمية للضوء The quantu thery f light الظاىرة الكهروضوئية Phtelectric effect لم تستطع الفيزياء الكالسيكية ونظرية موجية الضوء تفسير العديد من الظواىر الفيزيائية ومنها: طيف أشعة
الفصل الثاني عشر: النظرية الكمية للضوء The quantu thery f light الظاىرة الكهروضوئية Phtelectric effect لم تستطع الفيزياء الكالسيكية ونظرية موجية الضوء تفسير العديد من الظواىر الفيزيائية ومنها: طيف أشعة
2 nd Term Final Revision Sheet Students Name: Grade: 4 Subject: Saudi Culture Teacher Signature 1
 2 nd Term Final Revision Sheet Students Name: Grade: 4 Subject: Saudi Culture Teacher Signature 1 Saudi Culture Gr.4 راجعة اجتاعيات للصف الرابع االبتدائي 1 /الئي الجدول با يناسب ناخ كة الكرة )صيفا شتاء(ن
2 nd Term Final Revision Sheet Students Name: Grade: 4 Subject: Saudi Culture Teacher Signature 1 Saudi Culture Gr.4 راجعة اجتاعيات للصف الرابع االبتدائي 1 /الئي الجدول با يناسب ناخ كة الكرة )صيفا شتاء(ن
منتديات طموحنا * ملتقى الطلبة و الباحثين *
 منتديات طموحنا * ملتقى الطلبة و الباحثين * wwwtomohacom الكفاءات المستهدفة استعمال التمثيل البياني لتخمين سلوك ونهاية متتالية عددية دراسة سلوك ونهاية متتالية معرفة واستعمال مفهوم متتاليتين متجاورتين حل
منتديات طموحنا * ملتقى الطلبة و الباحثين * wwwtomohacom الكفاءات المستهدفة استعمال التمثيل البياني لتخمين سلوك ونهاية متتالية عددية دراسة سلوك ونهاية متتالية معرفة واستعمال مفهوم متتاليتين متجاورتين حل
( اختبارات الفروق لعينتين مستقلتين Samples) 2) Independent مان- ويتني( U (Mann-Whitney ب( نحتاج الى ھذا القانون الغراض المقارنة بين مجموعتين او عينتين
 ( اختارات الفروق لعينتين مستقلتين Samples) 2) Independent مان ويتني( U (MannWhitney ( نحتاج الى ھذا القانون الغراض المقارنة ين مجموعتين او عينتين مستقلتين مثال المقارنة ين عينة للذكور م ع عينة لالناث او
( اختارات الفروق لعينتين مستقلتين Samples) 2) Independent مان ويتني( U (MannWhitney ( نحتاج الى ھذا القانون الغراض المقارنة ين مجموعتين او عينتين مستقلتين مثال المقارنة ين عينة للذكور م ع عينة لالناث او
<4D F736F F D20C7E1CACDE1EDE120C7E1E3C7E1ED20E6C7E1DDE4ED>
 قسم الا بحاث والتقارير المالية التحليل المالي الخضري والفني التحليل المالي والفني لسهم الخضري نبذة عن الشركة يتمثل نشاط شركة أبناء عبدالله عبدالمحسن الخضري في تنفيذ مشاريع المقاولات العامة والتي تشمل مشاريع
قسم الا بحاث والتقارير المالية التحليل المالي الخضري والفني التحليل المالي والفني لسهم الخضري نبذة عن الشركة يتمثل نشاط شركة أبناء عبدالله عبدالمحسن الخضري في تنفيذ مشاريع المقاولات العامة والتي تشمل مشاريع
اليوم /
 طاقة رقم الموضوع : مفهو المجموعة. الهدف : ي عر ؼ المجموعة. تمهيد: ذكر كل مف : فوؿ النة. لواف عم فمطيف. الطال المحترموف. : كمل ما يتي : مثاؿ مف مثمة المجموعات : الخمفاء ال ارشدوف العداد الطيعية مف فر إلى
طاقة رقم الموضوع : مفهو المجموعة. الهدف : ي عر ؼ المجموعة. تمهيد: ذكر كل مف : فوؿ النة. لواف عم فمطيف. الطال المحترموف. : كمل ما يتي : مثاؿ مف مثمة المجموعات : الخمفاء ال ارشدوف العداد الطيعية مف فر إلى
بعض تطبيقات توازن جسم صلب خاضع لقوتين Quelques applications de l équilibre d un solide soumis à deux forces األدهاا *التذكير بشرطي توازن جسم صلب خاضع
 بعض تطبيقات توازن جسم صلب خاضع لقوتين Quelques applications de l équilibre d un solide soumis à deux forces األدهاا *التذكير بشرطي توازن جسم صلب خاضع لقوتين. *معرفة و تطبيق العالقة =T. K *تعريف دافعة أرخمياس
بعض تطبيقات توازن جسم صلب خاضع لقوتين Quelques applications de l équilibre d un solide soumis à deux forces األدهاا *التذكير بشرطي توازن جسم صلب خاضع لقوتين. *معرفة و تطبيق العالقة =T. K *تعريف دافعة أرخمياس
مكثف الثالثة الوحدة البوابات املنطقية 1 هاتف : مدارس األكاد م ة العرب ة الحد ثة إعداد المعلم أحمد الصالح
 مكثف الثالثة الوحدة البوابات املنطقية هاتف : 798226 النظ ري الج زء و الثاني األ ول للد رسين وضح ان قصىد ت ا يهي : انرعثير انعالئقي ج هح خثريح ذكى قي رها إيا صىاب )( و إيا خطأ )( ان عايم ان طقي راتط يسرخذو
مكثف الثالثة الوحدة البوابات املنطقية هاتف : 798226 النظ ري الج زء و الثاني األ ول للد رسين وضح ان قصىد ت ا يهي : انرعثير انعالئقي ج هح خثريح ذكى قي رها إيا صىاب )( و إيا خطأ )( ان عايم ان طقي راتط يسرخذو
اختبار تحليل التباين األحادي و اختبار كرودكال والس الالمعلمي يبين السؤال التالي ست مجموعات من دول العالم توضح نسبة التحضر في كل منها حسب الموجود في ال
 اختبار تحليل التباين األحادي و اختبار كرودكال والس الالمعلمي يبين السؤال التالي ست مجموعات من دول العالم توضح نسبة التحضر في كل منها حسب الموجود في الملفات الثالثة المرفقة المطلوب : 1 -هل وجد اختالف ب
اختبار تحليل التباين األحادي و اختبار كرودكال والس الالمعلمي يبين السؤال التالي ست مجموعات من دول العالم توضح نسبة التحضر في كل منها حسب الموجود في الملفات الثالثة المرفقة المطلوب : 1 -هل وجد اختالف ب
Microsoft Word - متوازي الأضلاع .docx
 التوازي والتعامد التماثل المركزي المكتسبات القبلیة الكفایات توجیھات تربویة التعرف على متوازي الا ضلاع و خاصیاتھ المتعلقة بالا ضلاع و الزوایا ربط خاصیات متوازي الا ضلاع بالتماثل المركزي. یعتبر التماثل المركزي
التوازي والتعامد التماثل المركزي المكتسبات القبلیة الكفایات توجیھات تربویة التعرف على متوازي الا ضلاع و خاصیاتھ المتعلقة بالا ضلاع و الزوایا ربط خاصیات متوازي الا ضلاع بالتماثل المركزي. یعتبر التماثل المركزي
المحاضرة الثانية
 المحاضرة الثان ة أنواع الب انات)المتغ رات و الثوابت( محتو ات المحاضرة أنواع الب انات اإلعالن عن المتغ رات الثوابت إسناد الق م إلى المتغ رات واجهة برنامج Visual Studio 2010 2 أنواع الب انات كلمات لغة ال
المحاضرة الثان ة أنواع الب انات)المتغ رات و الثوابت( محتو ات المحاضرة أنواع الب انات اإلعالن عن المتغ رات الثوابت إسناد الق م إلى المتغ رات واجهة برنامج Visual Studio 2010 2 أنواع الب انات كلمات لغة ال
1 ère Collège_CE7 Devoir Surveillé n : 1A-S1-Ar 15/10/2010 Page : 1/1 Exercice.1 calculer en écrivant les étapes intermédiaires A = B = 3 +
 ère ollège_e evoir Surveillé n : -S-r // Page : / = + = + = 4 + 4 4 + 4 التم ين أحسب ما يلي مع كتابة الم احل الوسطية =. = ( + 4) = 4 التم ين. أحسب ما يلي مع كتابة الم احل الوسطية points) 4) = + ( ) = (
ère ollège_e evoir Surveillé n : -S-r // Page : / = + = + = 4 + 4 4 + 4 التم ين أحسب ما يلي مع كتابة الم احل الوسطية =. = ( + 4) = 4 التم ين. أحسب ما يلي مع كتابة الم احل الوسطية points) 4) = + ( ) = (
مقدمة عن الاوناش
 مقدمة عن االوناش مهندس اعداد / ناصر محمود احمد االوناش Cranes هي نوع من المعدات تستخدم لرفع وخفض ونقل االحمال الكبيرة. المبادئ الميكانيكية االساسية لالوناش:- قدرة الونش علي رفع الحمولة. 1. عدم سقوط الونش
مقدمة عن االوناش مهندس اعداد / ناصر محمود احمد االوناش Cranes هي نوع من المعدات تستخدم لرفع وخفض ونقل االحمال الكبيرة. المبادئ الميكانيكية االساسية لالوناش:- قدرة الونش علي رفع الحمولة. 1. عدم سقوط الونش
أاعمال الر سل 507
 أاعمال الر سل 507 أاعمال الر سل 508 أاعمال الر سل 509 أاعمال الر سل امل ق د م ة 1 اإن ق دج أ نج ش اأ ج ت ال ك الم الأ و ل ي ا ث او ف ي ل س ف ج م يع الأ م ور ال ت ي ابج ت د اأ ي س وع يعج م ل ه ا و ي ع ل
أاعمال الر سل 507 أاعمال الر سل 508 أاعمال الر سل 509 أاعمال الر سل امل ق د م ة 1 اإن ق دج أ نج ش اأ ج ت ال ك الم الأ و ل ي ا ث او ف ي ل س ف ج م يع الأ م ور ال ت ي ابج ت د اأ ي س وع يعج م ل ه ا و ي ع ل
Microsoft Word - Study Plan _ Arabic
 البرنامج الا سترشادي لطلبة قسم الهندسة الميكانيكية السنة الا ولى (جميع التخصصات: قوى حرارية ميكاترونكس طيران) رمز ورقم رمز ورقم المساق المساق - لغة عربية ع 101 - مهارات الحاسوب ن م 100 ر 101 تفاضل وتكامل
البرنامج الا سترشادي لطلبة قسم الهندسة الميكانيكية السنة الا ولى (جميع التخصصات: قوى حرارية ميكاترونكس طيران) رمز ورقم رمز ورقم المساق المساق - لغة عربية ع 101 - مهارات الحاسوب ن م 100 ر 101 تفاضل وتكامل
الواجب المنزلي: اسم الطالب: السؤال األول : أكمل العبارات التالية بما يناسبها: 1- نصف المسافة بين نواتي ذرتين متجاورتين )...( 2- الطاقة الالزمة لنزع اإ
 الواجب المنزلي: اسم الطالب: السؤال األول : أكمل العبارات التالية بما يناسبها: 1- نصف المسافة بين نواتي ذرتين متجاورتين )...( 2- الطاقة الالزمة لنزع اإللكترون من الذرة المفردة وهي في الحالة الغازية )...(
الواجب المنزلي: اسم الطالب: السؤال األول : أكمل العبارات التالية بما يناسبها: 1- نصف المسافة بين نواتي ذرتين متجاورتين )...( 2- الطاقة الالزمة لنزع اإللكترون من الذرة المفردة وهي في الحالة الغازية )...(
اسم المدرس: رقم المكتب: الساعات المكتبية: موعد المحاضرة: جامعة الزرقاء الكمية: الحقوق عدد الساعات: 3 ساعات معتمدة نوع المتطمب: تخصص اختياري عنوان المق
 اسم المدرس: رقم المكتب: الساعات المكتبية: موعد المحاضرة: جامعة الزرقاء الكمية: الحقوق عدد الساعات: 3 ساعات معتمدة نوع المتطمب: تخصص اختياري عنوان المقرر: ج ارئم تكنولوجيا المعمومات )0602344( المتطمب السابق:
اسم المدرس: رقم المكتب: الساعات المكتبية: موعد المحاضرة: جامعة الزرقاء الكمية: الحقوق عدد الساعات: 3 ساعات معتمدة نوع المتطمب: تخصص اختياري عنوان المقرر: ج ارئم تكنولوجيا المعمومات )0602344( المتطمب السابق:
عرض تقديمي في PowerPoint
 Dr./ Ahmed Mohamed Rabie Sayed 1 2 صندوق االدوات صندوق االدوات Tools Box يحتوى اظهار وإخفاء Tools Box من قائمة على االدوات Window الرئيسية الالزمة النشاء واختيار.Tools وتعديل التصميم. ويمكن 3 Move Tool
Dr./ Ahmed Mohamed Rabie Sayed 1 2 صندوق االدوات صندوق االدوات Tools Box يحتوى اظهار وإخفاء Tools Box من قائمة على االدوات Window الرئيسية الالزمة النشاء واختيار.Tools وتعديل التصميم. ويمكن 3 Move Tool
1
 1 اهلل ال ح س ن ى ماء أ س م ن ظ و مة في للشيخ العالمة زيد بن محمد بن ىادي المدخلي رحمو اهلل - 2 . اهلل رحمن ر حيم غاف ر...وحاف ظ ح ي ح ليم ناص ر. وخال ق وبار ئ م ه يم ن...ثم ل طيف م حس ن وم ؤ م ن. وم ان
1 اهلل ال ح س ن ى ماء أ س م ن ظ و مة في للشيخ العالمة زيد بن محمد بن ىادي المدخلي رحمو اهلل - 2 . اهلل رحمن ر حيم غاف ر...وحاف ظ ح ي ح ليم ناص ر. وخال ق وبار ئ م ه يم ن...ثم ل طيف م حس ن وم ؤ م ن. وم ان
جامعة حضرموت
 جاهعة حضرهوت التسجيل االلكتروني لمرحلة التنسيق بالجامعة عبر الموقع www.hu-registration.com الصفحة الرئيسية زر الدخول على النظام ف حالة التسج ل سابقا ولد ك اسم مستخدم وكلمة مرور زر تسج ل متقدم جد د اذا
جاهعة حضرهوت التسجيل االلكتروني لمرحلة التنسيق بالجامعة عبر الموقع www.hu-registration.com الصفحة الرئيسية زر الدخول على النظام ف حالة التسج ل سابقا ولد ك اسم مستخدم وكلمة مرور زر تسج ل متقدم جد د اذا
جامعة دمشق كلية الهندسة المدنية السنة الثالثة ملخص مادة الهيدروجيولوجيا Written by : Ammar najjar مكتبة الخدمات الطالبية )الكشك( 1 Ammoury
 جامعة دمشق كلية الهندسة المدنية السنة الثالثة ملخص مادة الهيدروجيولوجيا Written by : Ammar najjar 1 يعتبر علم الهيدروجبولوجبا من العلوم الهامة في مجال الهندسة المدنية وهو يدرس بشكل أساسي المياه الجوفية
جامعة دمشق كلية الهندسة المدنية السنة الثالثة ملخص مادة الهيدروجيولوجيا Written by : Ammar najjar 1 يعتبر علم الهيدروجبولوجبا من العلوم الهامة في مجال الهندسة المدنية وهو يدرس بشكل أساسي المياه الجوفية
الفصل الثامن: تكاليف الإنتاج في الأجل القصير
 عرض المنشاة في سوق االحتكار التام) 18 ( Pure Monopoly مقدمة االحتكار التام احد اشكال السوق غير التنافسية الذي يكون فية بائع )منتج( واحد لسلعة او خدمة وعدد كبير من المشتريين.ويتحكم هذا البائع بشكل تام في
عرض المنشاة في سوق االحتكار التام) 18 ( Pure Monopoly مقدمة االحتكار التام احد اشكال السوق غير التنافسية الذي يكون فية بائع )منتج( واحد لسلعة او خدمة وعدد كبير من المشتريين.ويتحكم هذا البائع بشكل تام في
وضح أهمية وصف مظاهر التكوينات الجديدة فى التربة فى مجال مورفولوجيا الأراضى
 كلية الزراعة- قسم األراضى والمياه أمتحان الفصل الدراسى االول للعام الجامعى /1012 1015 تاريخ االمتحان : 15 1012 / 2 / شعبة / األراضى الفرقة / الرابعة الزمن / ساعتين أسم المادة/ االستشعار عن بعد فى الزراعة
كلية الزراعة- قسم األراضى والمياه أمتحان الفصل الدراسى االول للعام الجامعى /1012 1015 تاريخ االمتحان : 15 1012 / 2 / شعبة / األراضى الفرقة / الرابعة الزمن / ساعتين أسم المادة/ االستشعار عن بعد فى الزراعة
